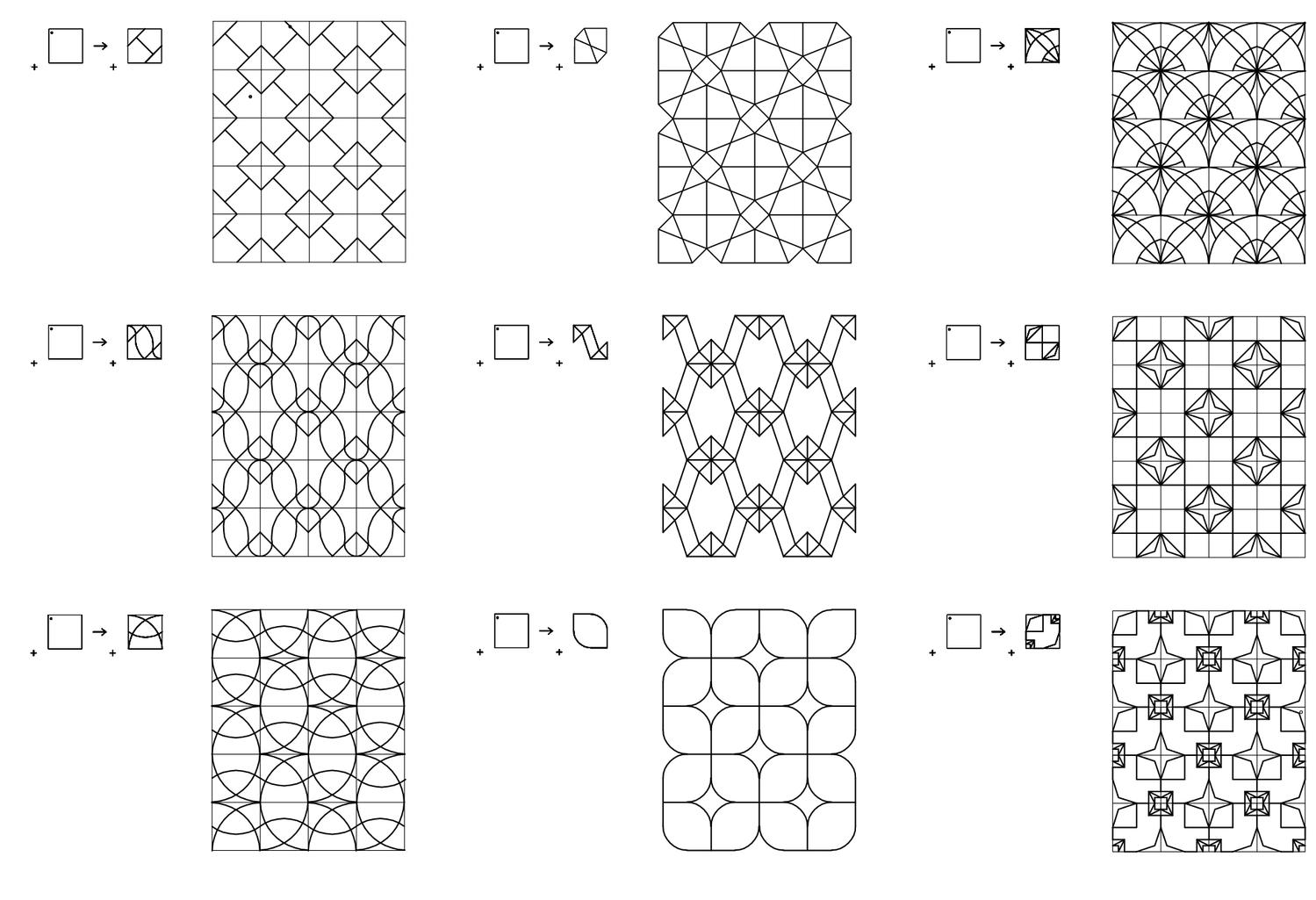
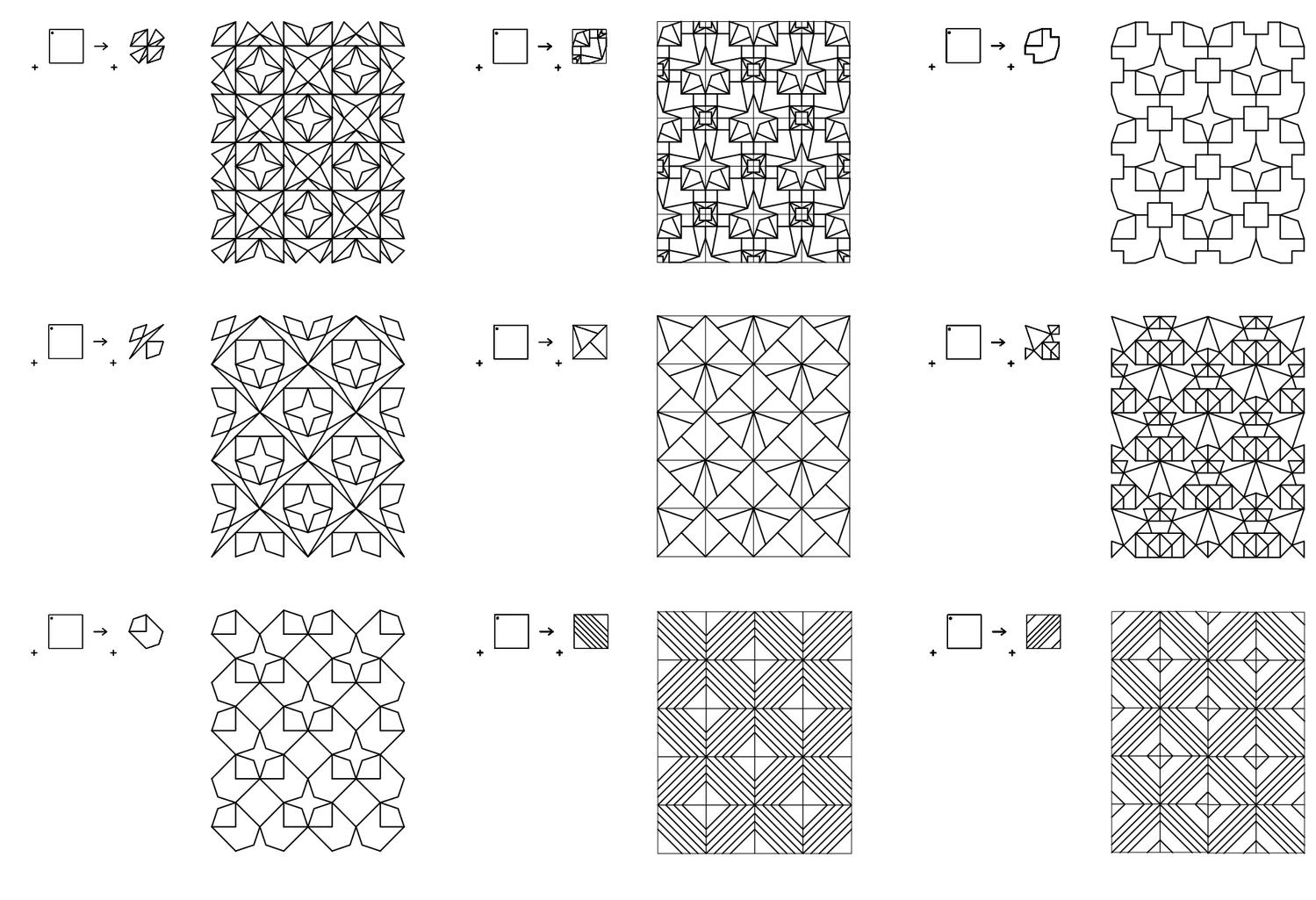
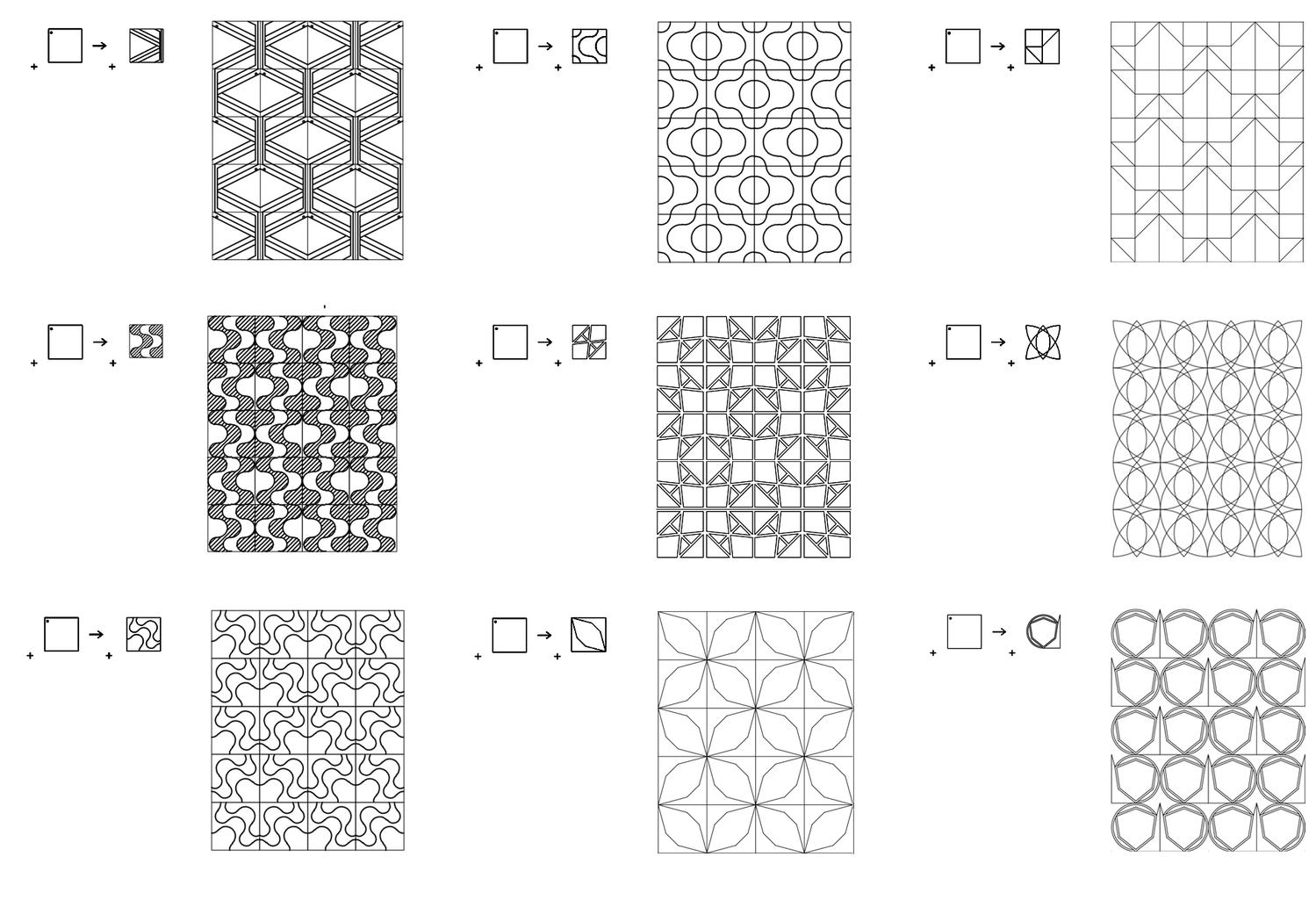
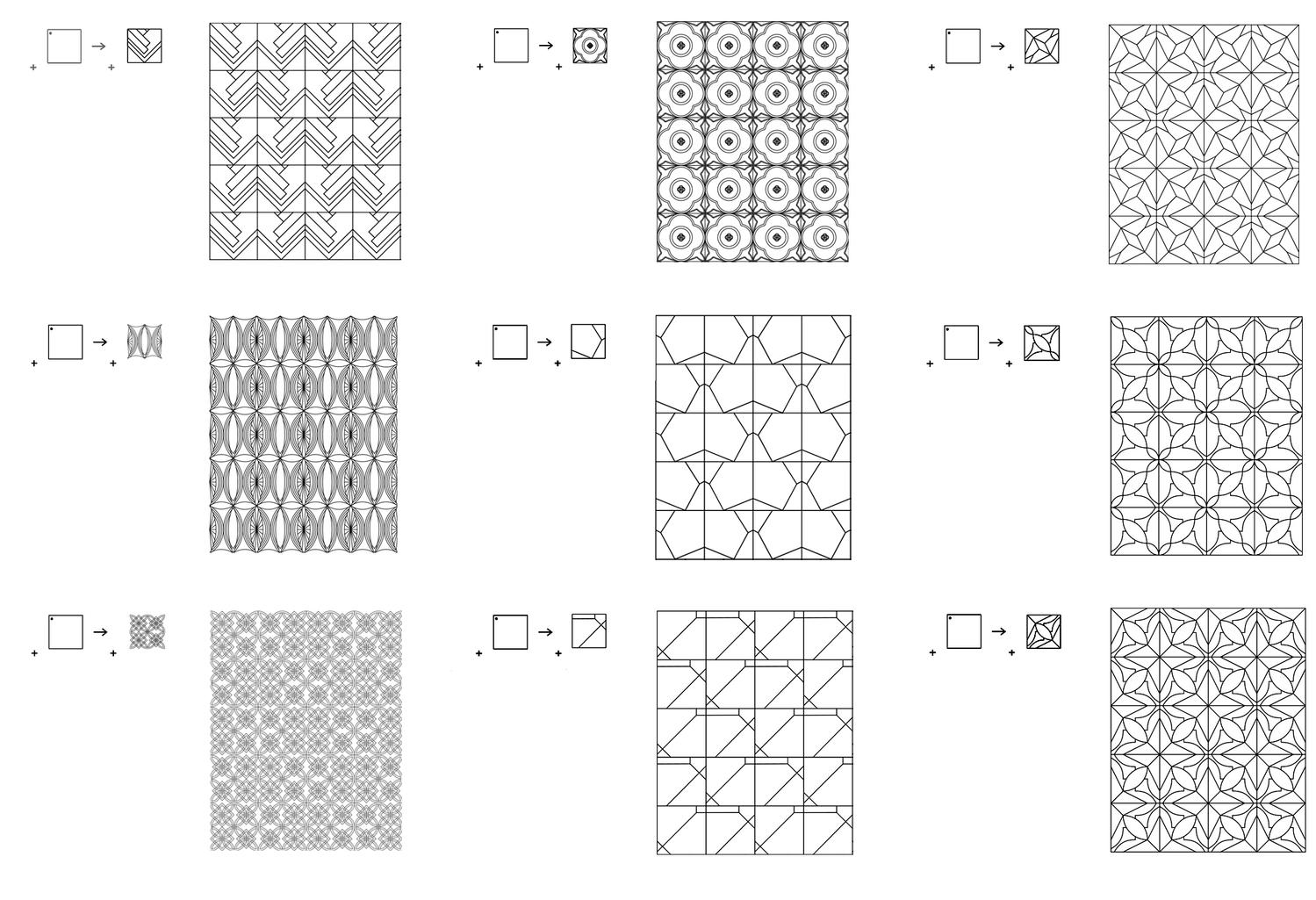
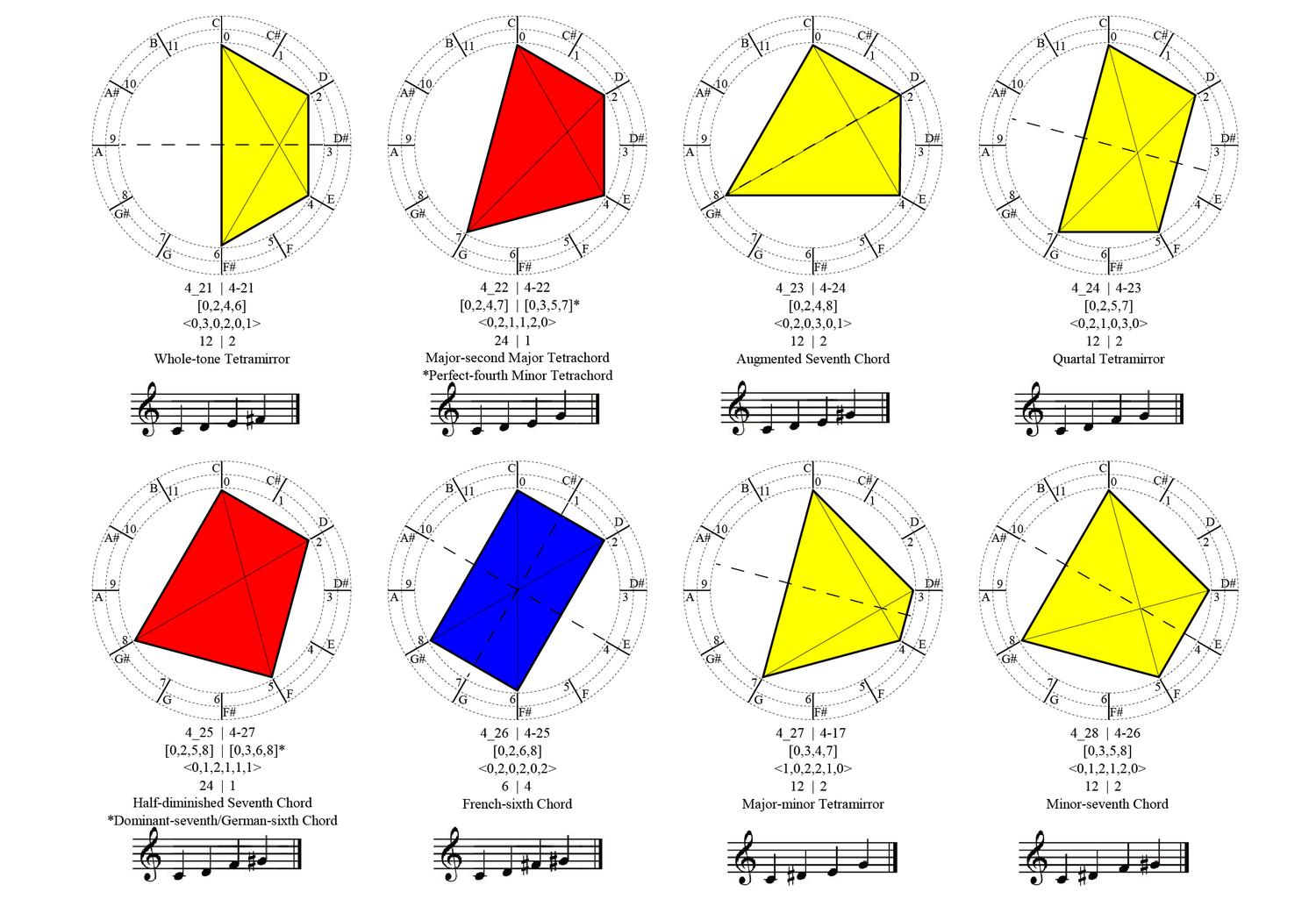
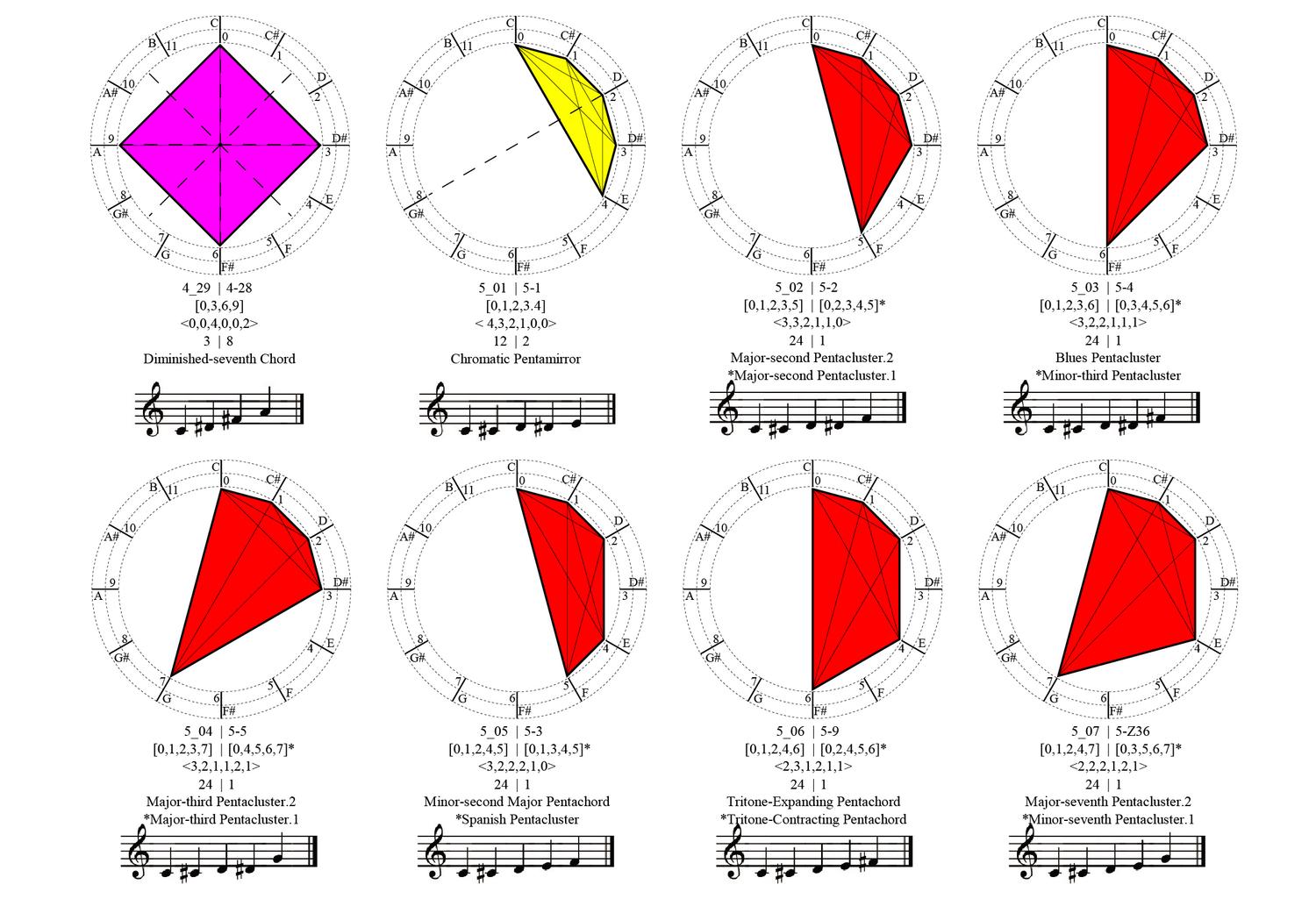
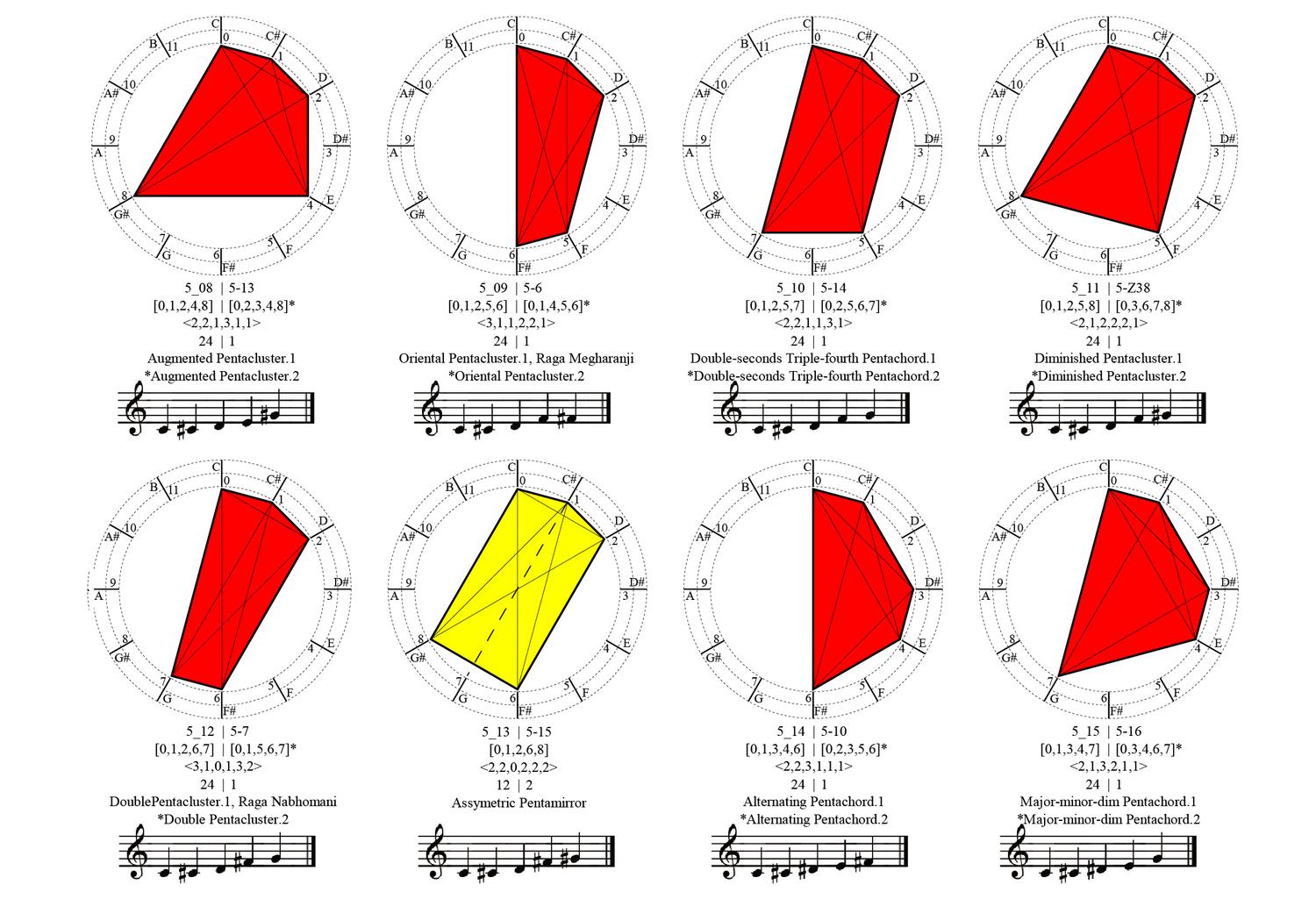
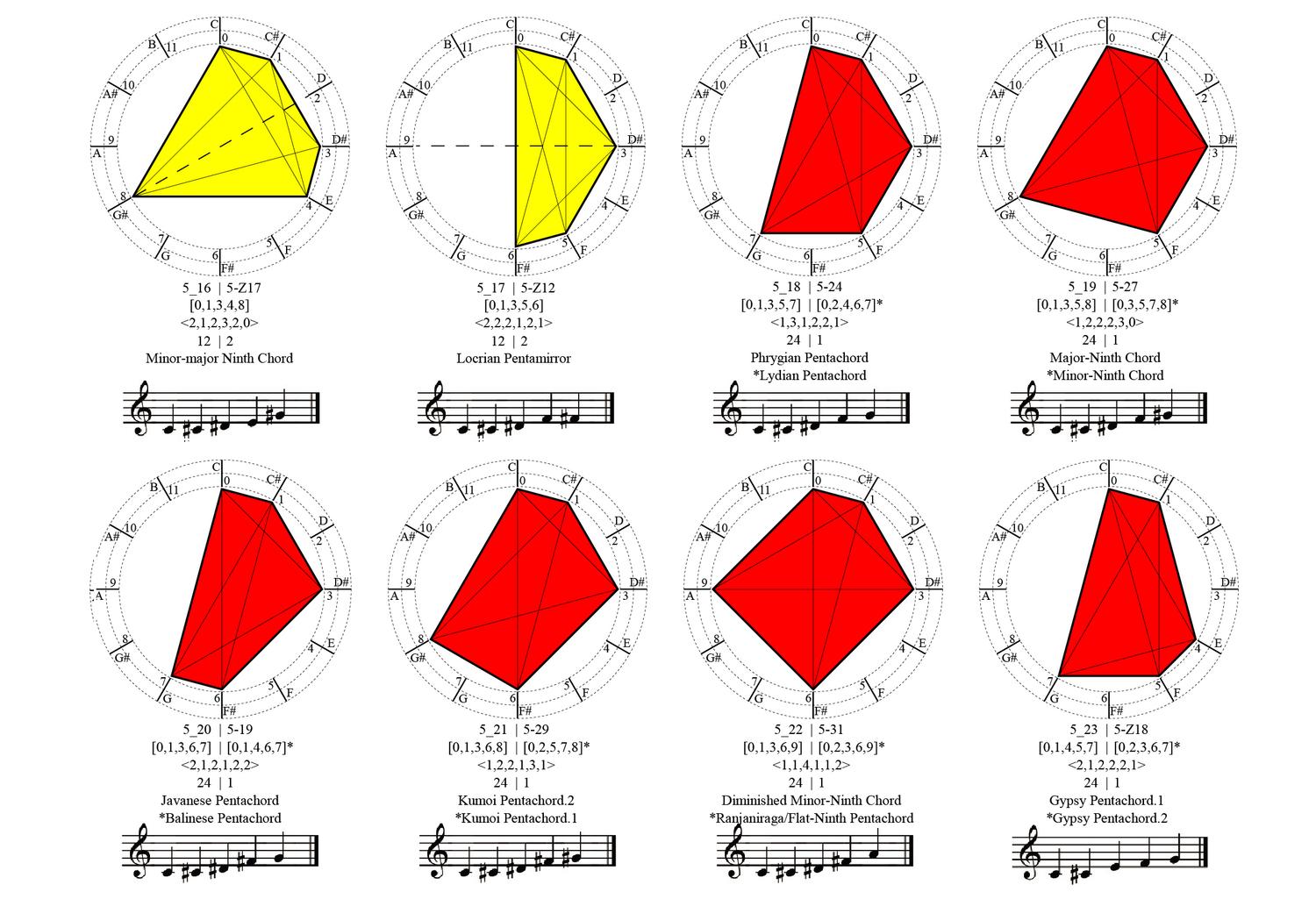
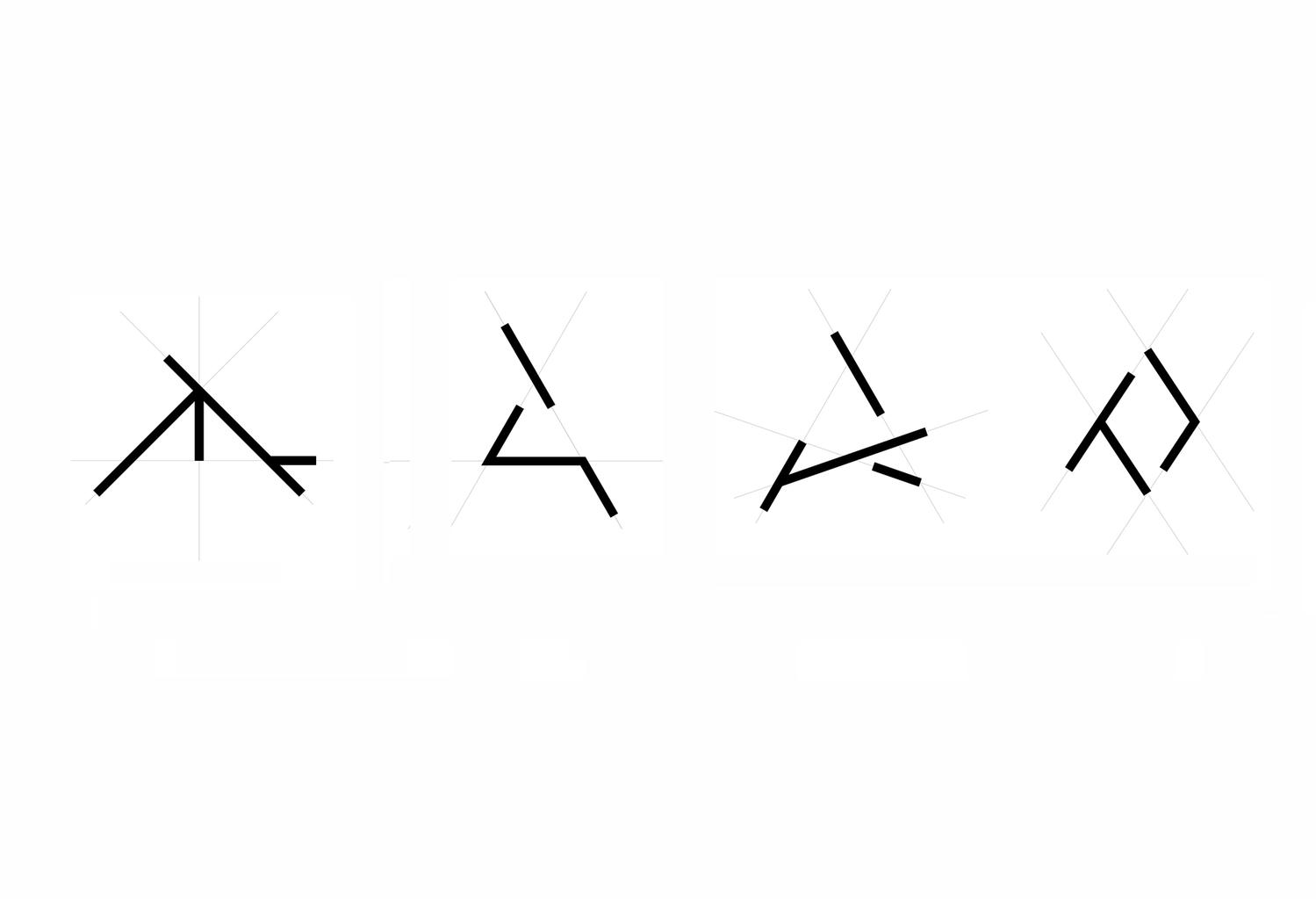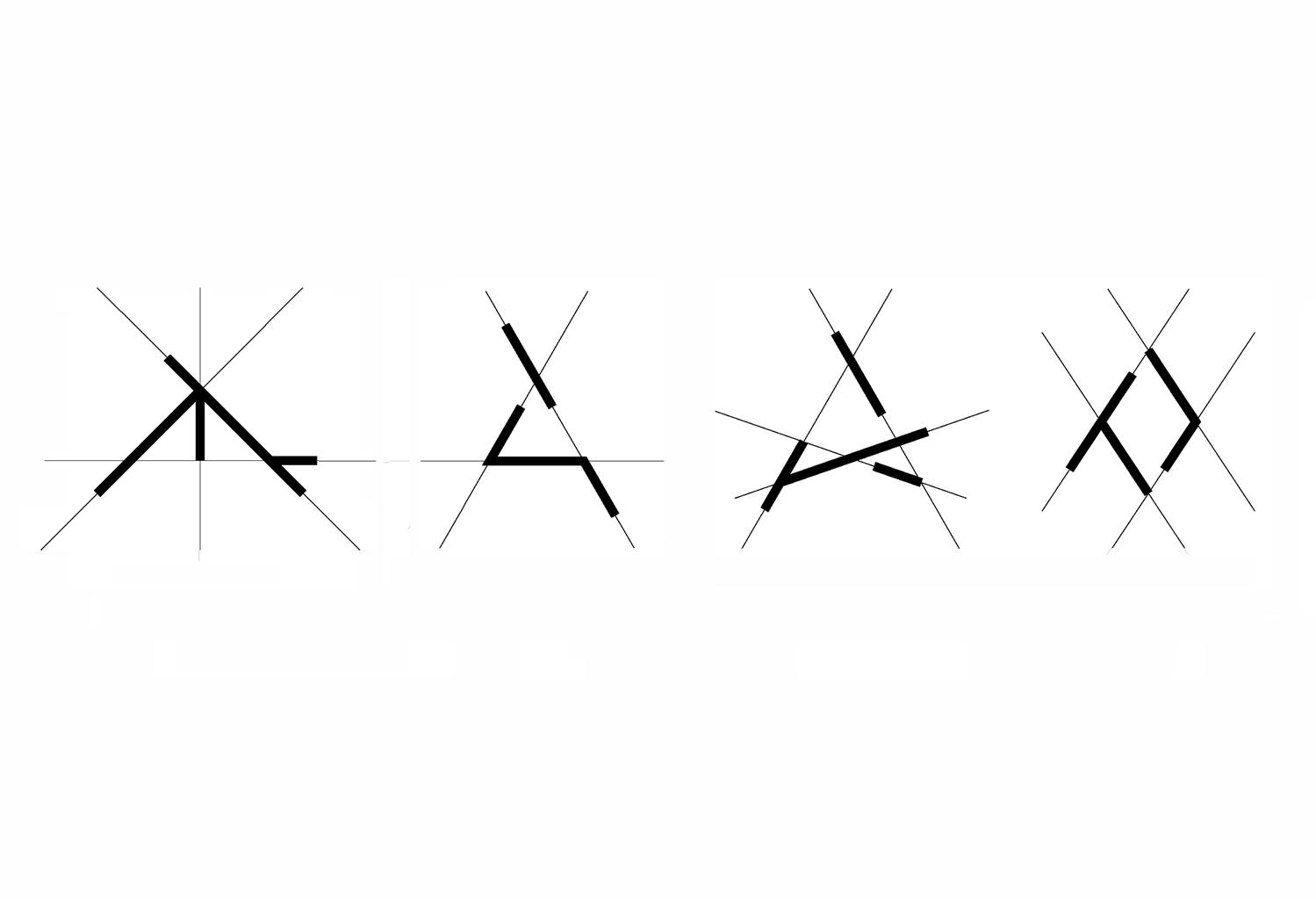Shape Signature
Athanassios Economou, Josephine Yu and James Park
2019
Keywords: Lines; Matroids; Chirotopes; Polya's theorem of Enumeration; Figurative numbers; Symmetry; Mathematica
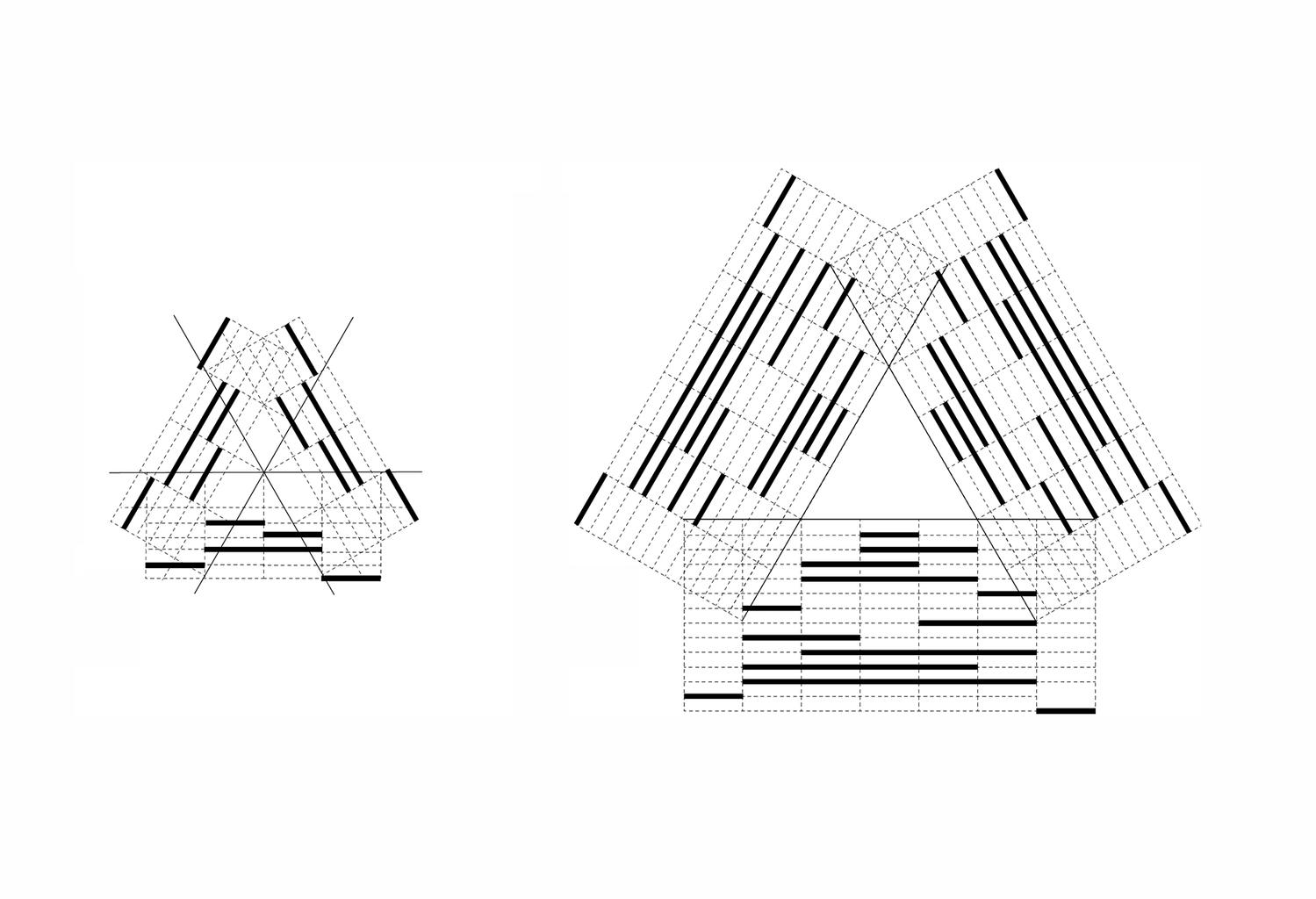
Shape Signature provides a new and uniform specification of parametric shapes consisting of points, lines, planes and solids. The model extends the shape grammar definition of a shape consisting of maximal elements of lines, planes and solids to the specification of parametric shapes consisting of maximal elements of lines, planes and solids to ultimately ensure that a specification of a parametric shape is unique - and even more, captured by a numerical formula. The method proceeds from considering a shape consisting of a collection of maximal lines upon an arrangement of hyperplanes to calculate and visually represent any parametric shape consisting of lines in CAD parametric models.
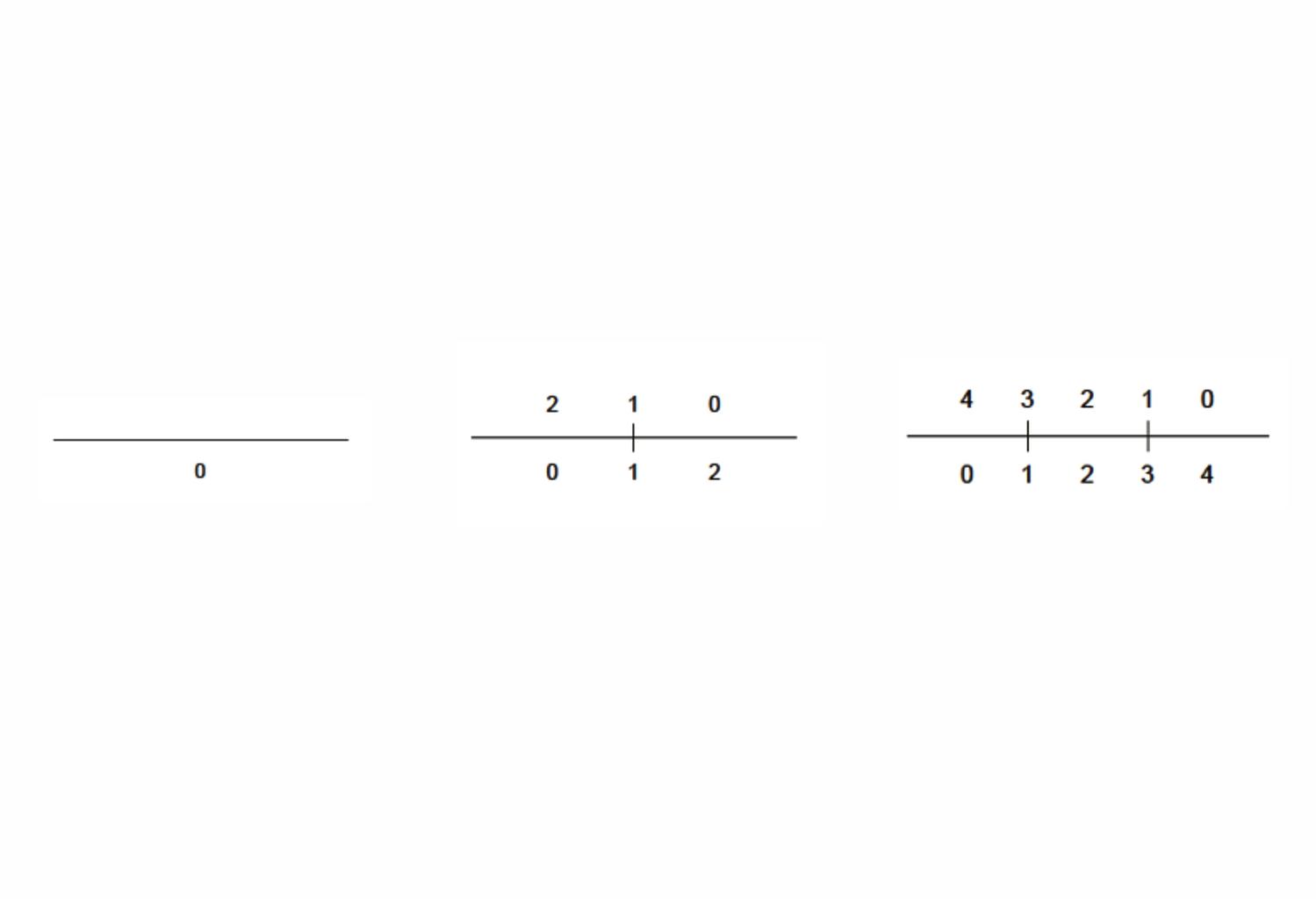
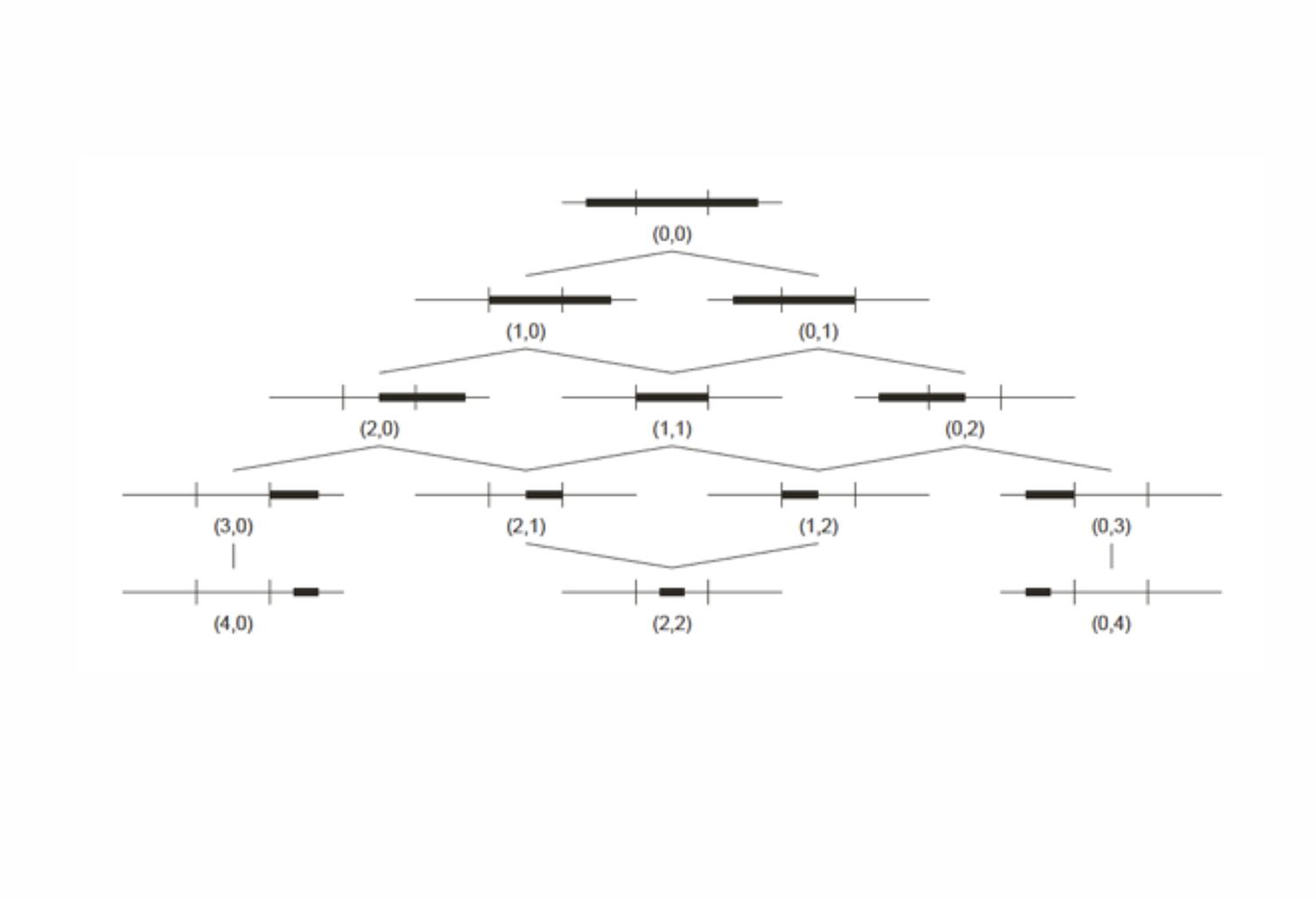
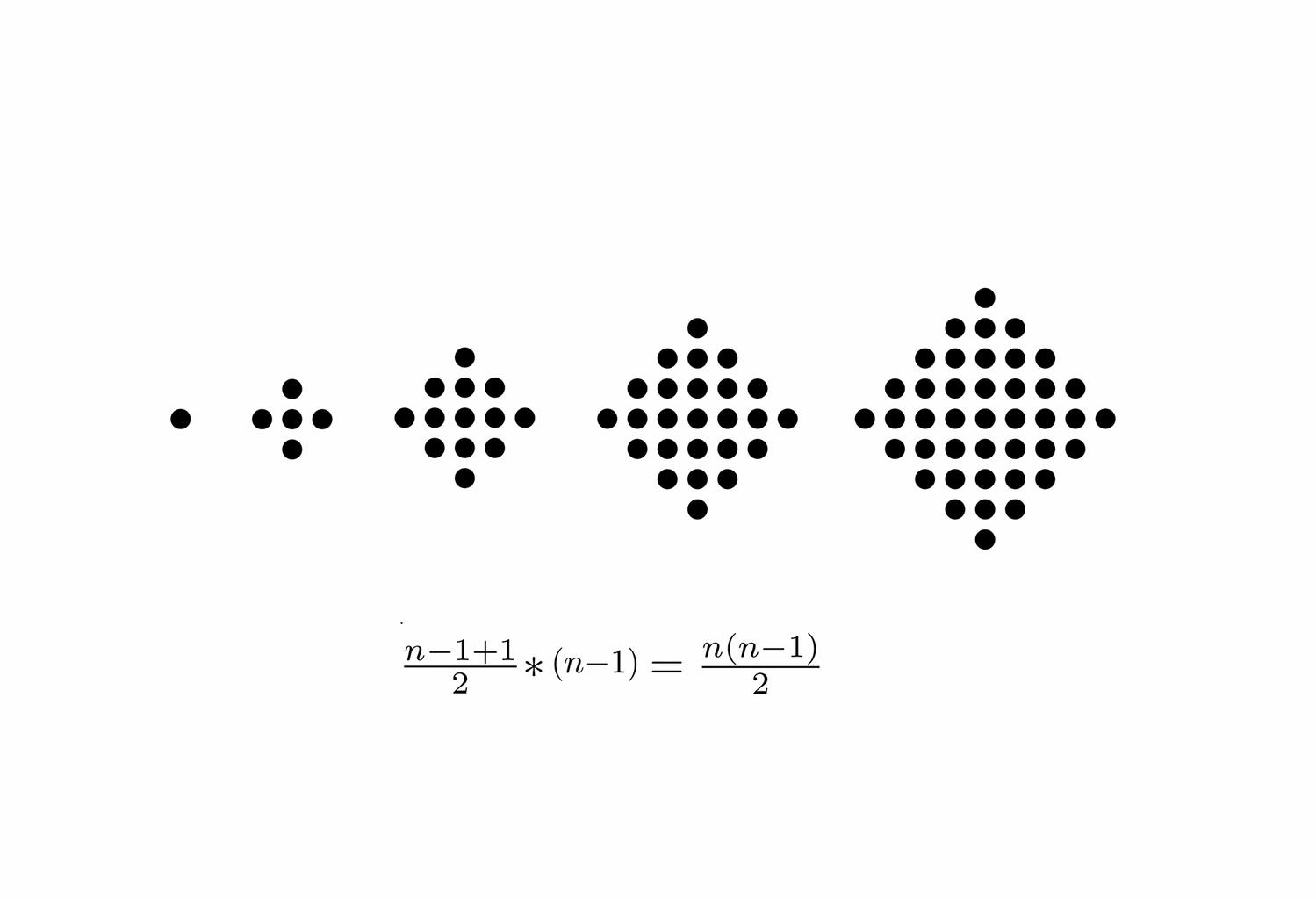
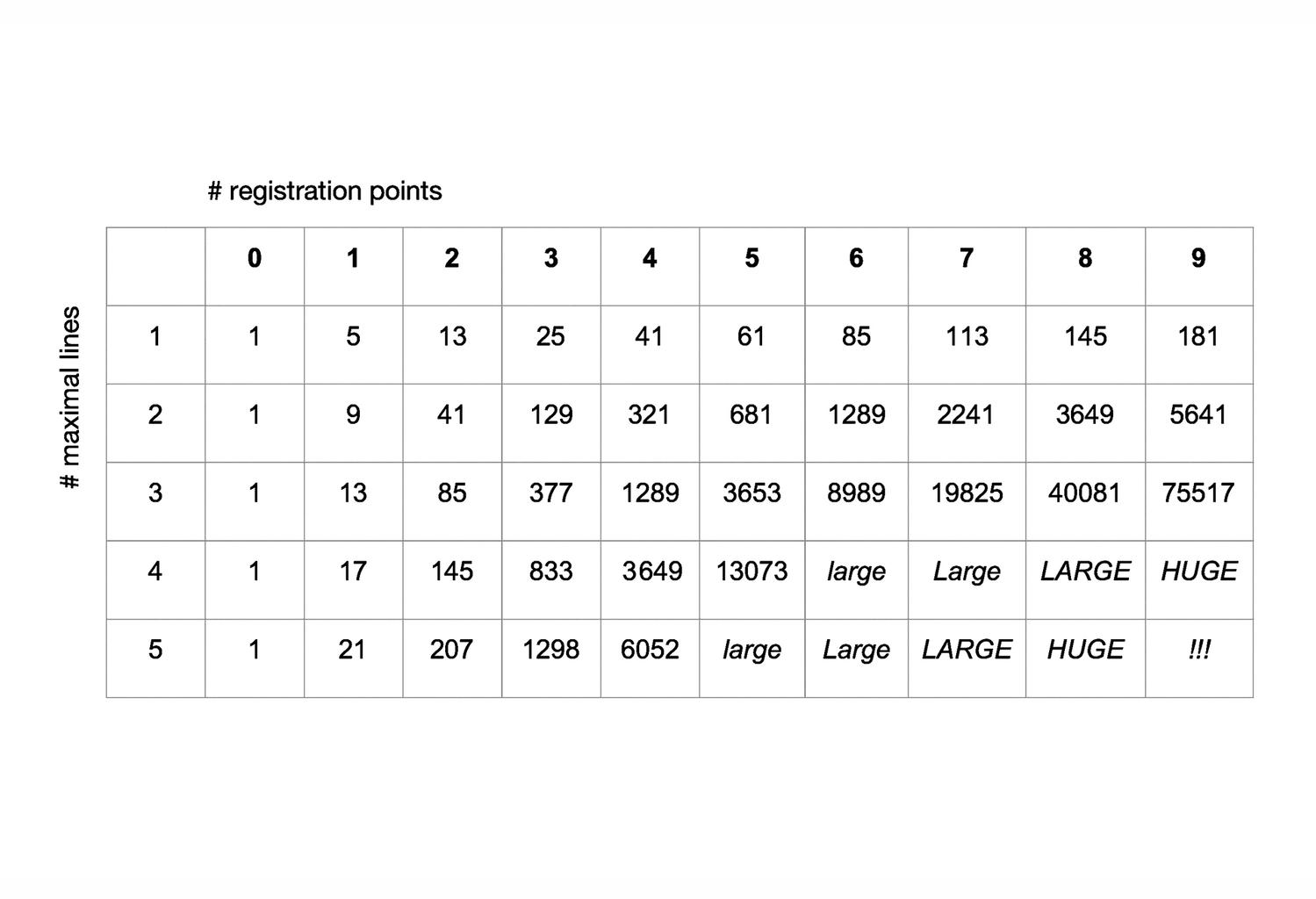
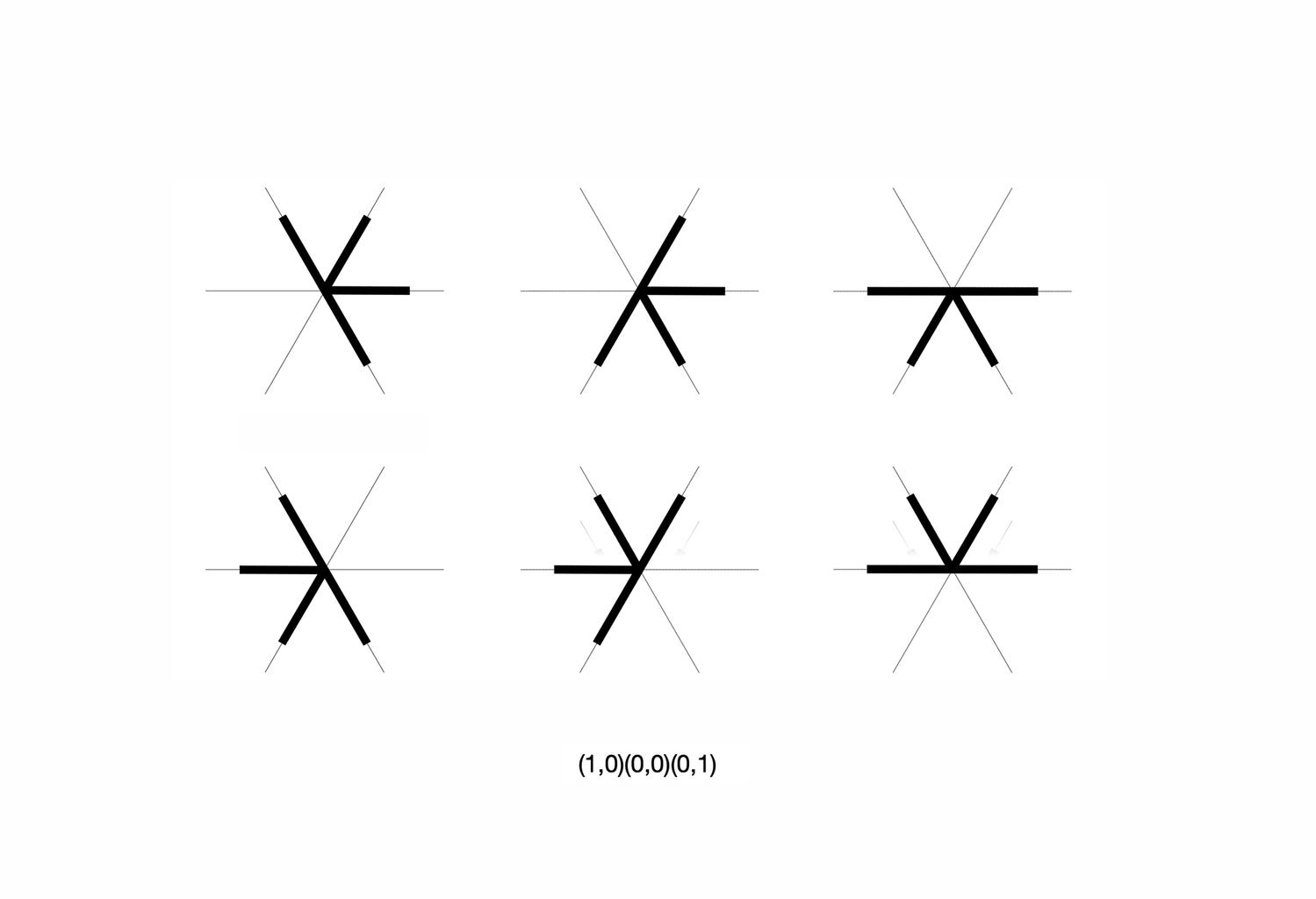
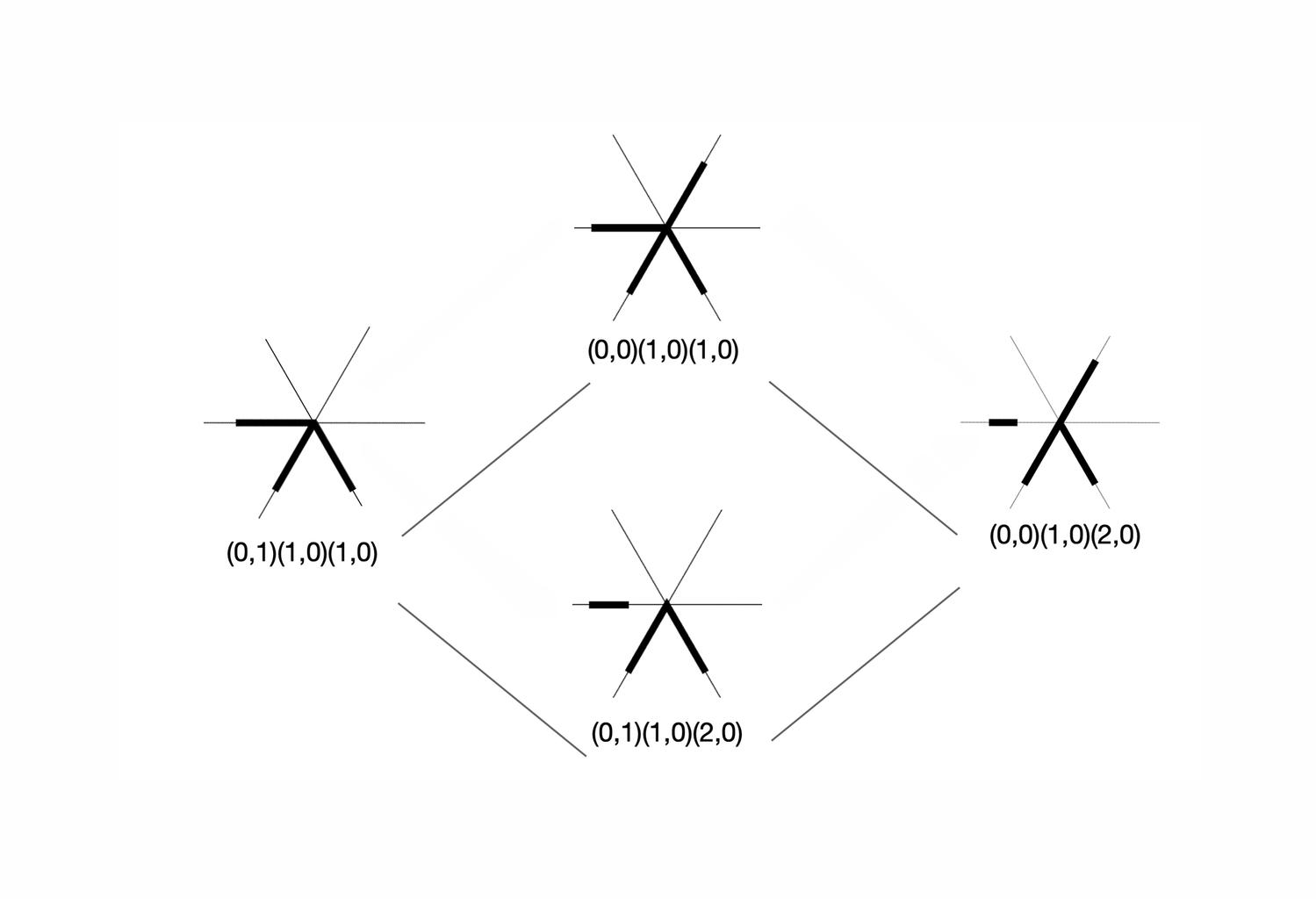
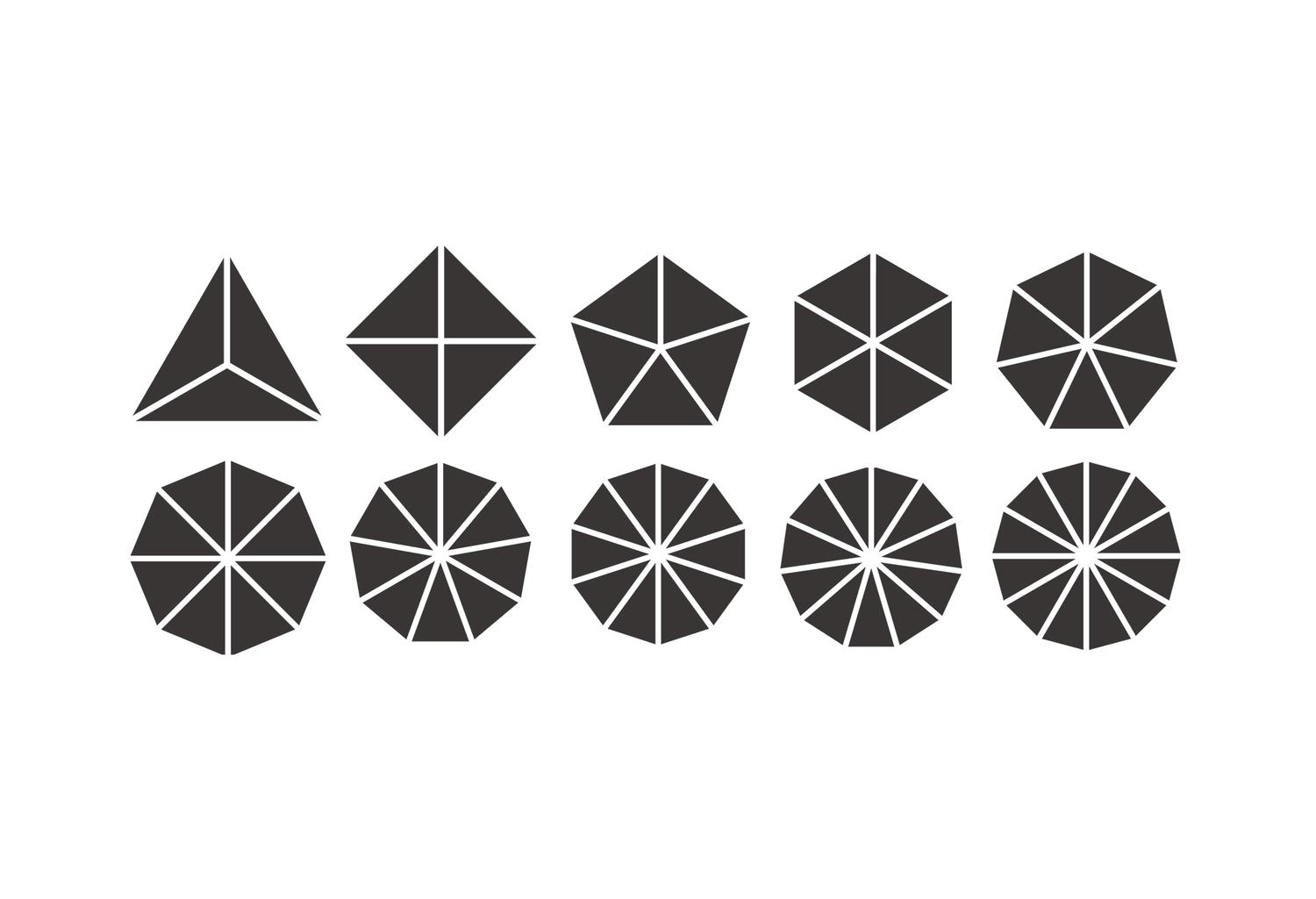
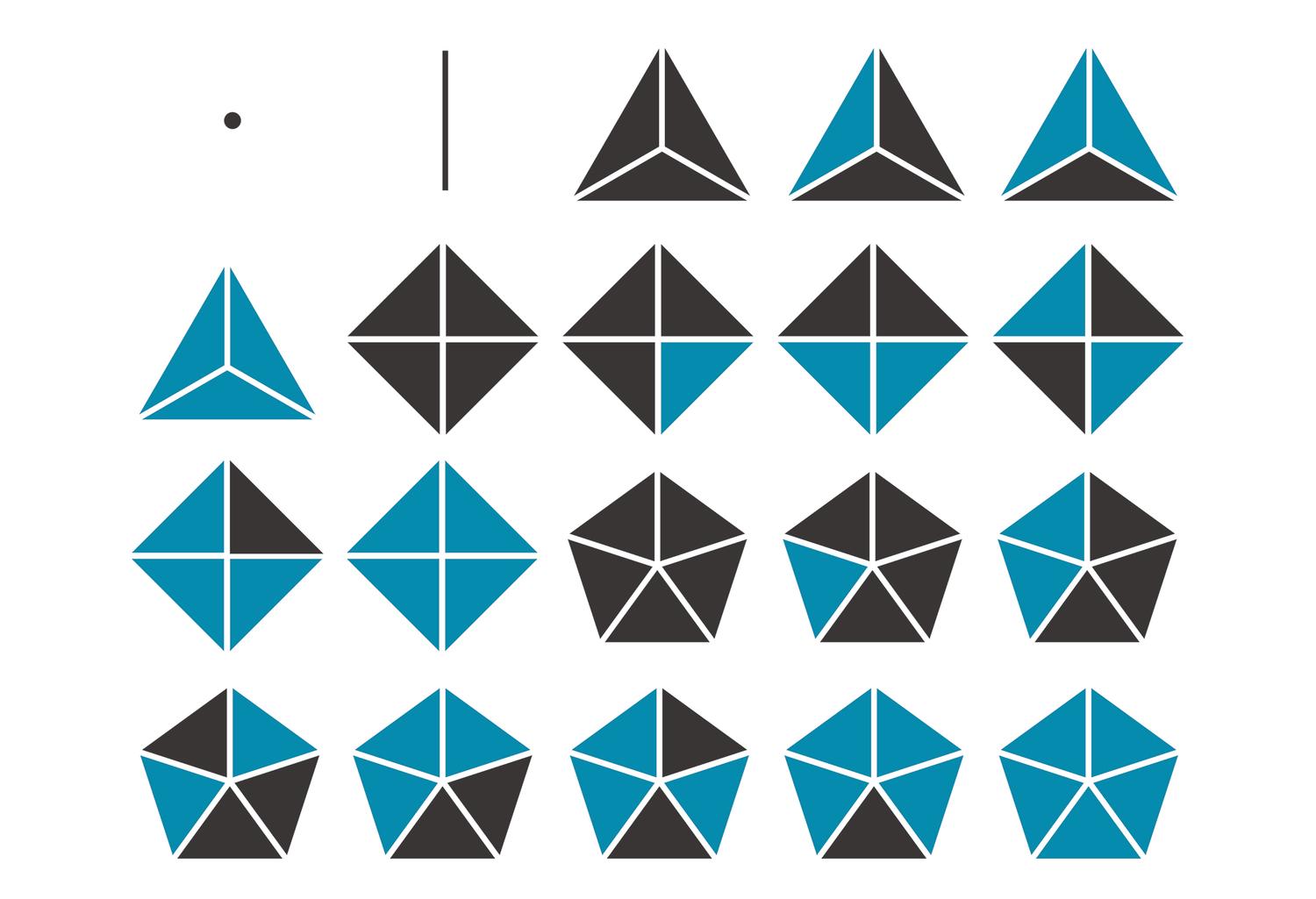
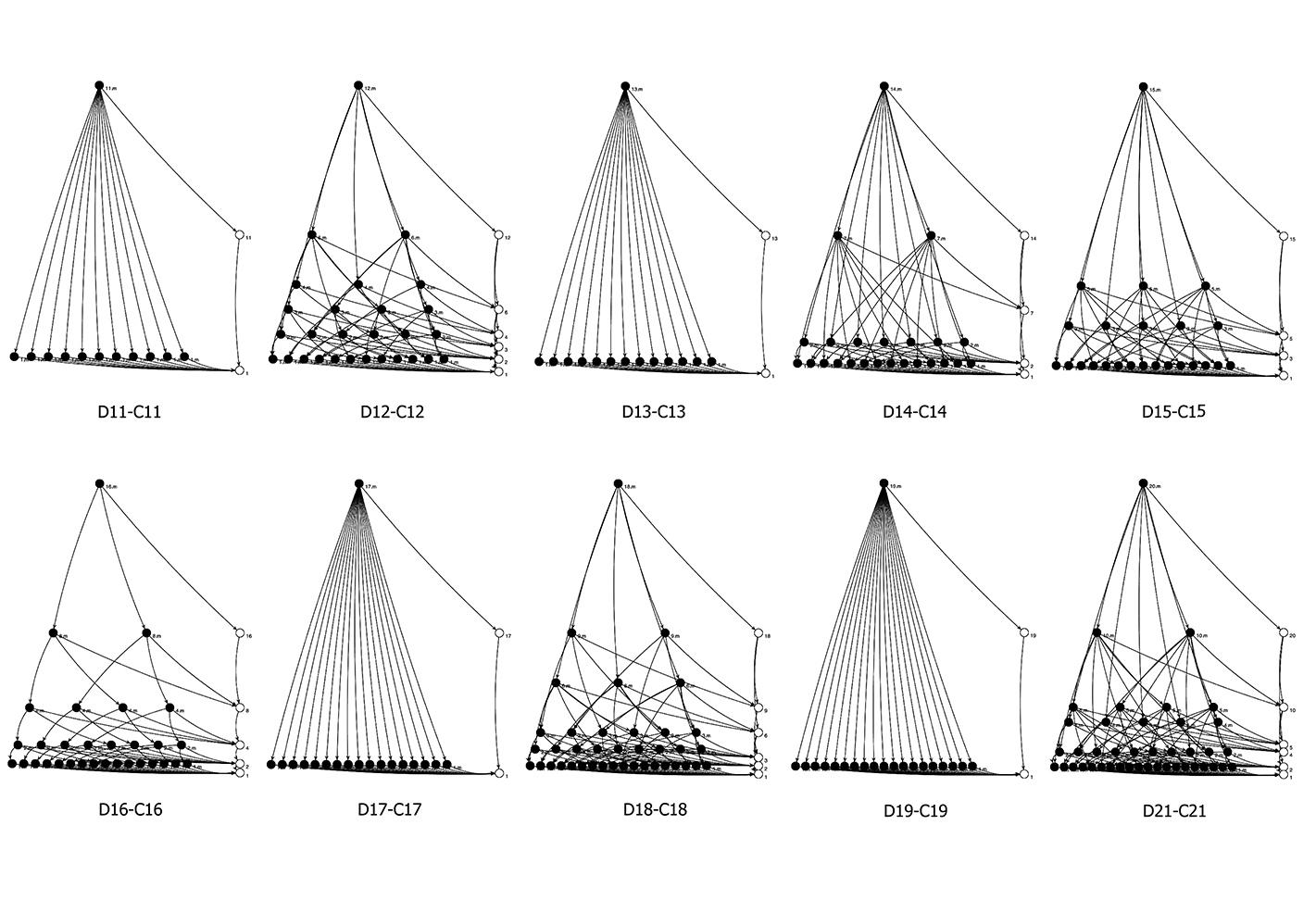
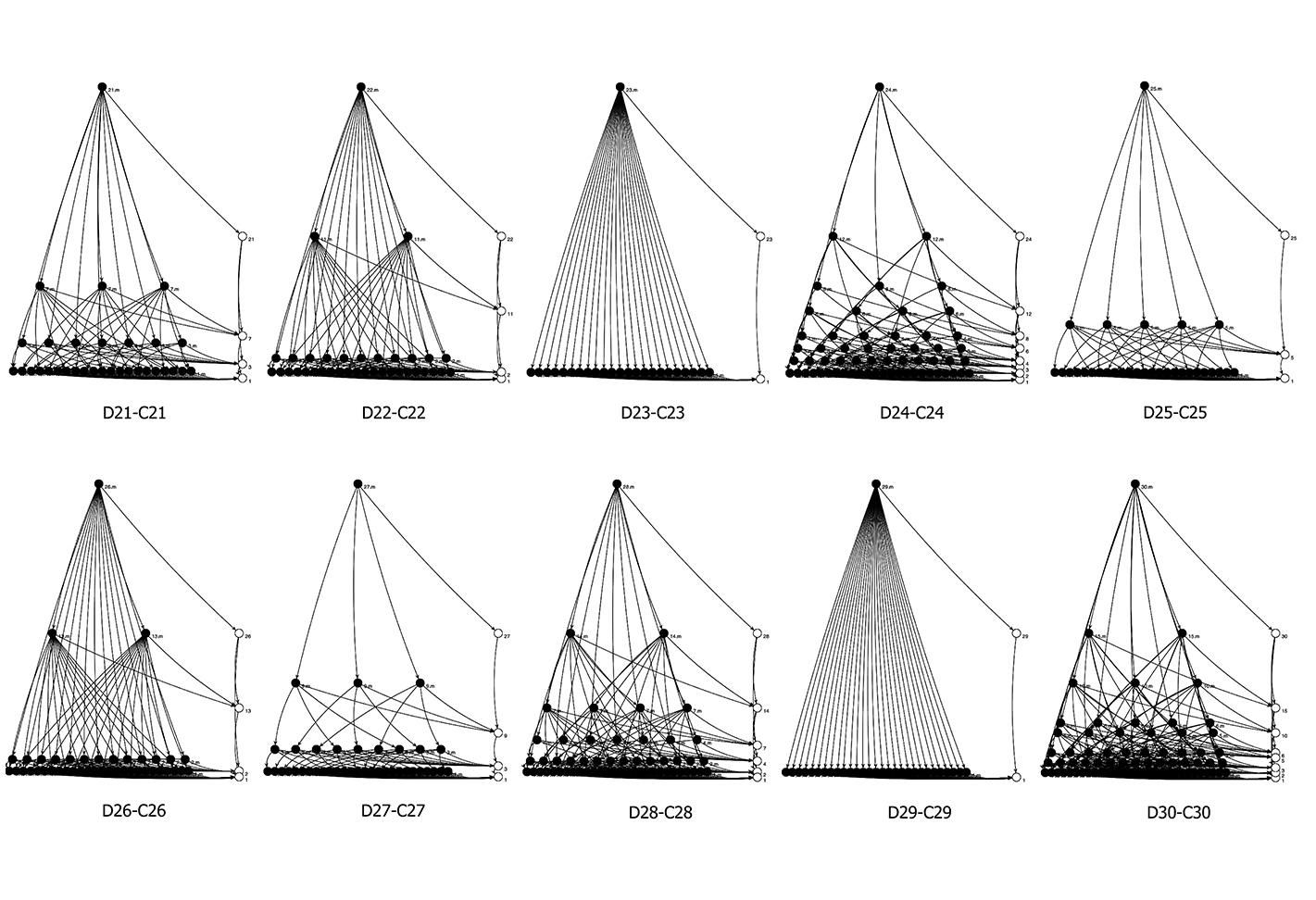
A key idea in the shape signature is the indefinite number of parts in a maximal element. This number is only defined with respect to the context where a maximal element is. For example, a line when it is in no spatial relation with some other line, it has 1 unlimited number of parts; the same line may have up to 5 parts when it is in a spatial relation with another line; 13 parts with 2 lines; 41 parts with 4 lines; and so forth, following the sequence of centered square figurate numbers and their corresponding powers in higher dimensions for more elaborate combinations of number of parts per line.
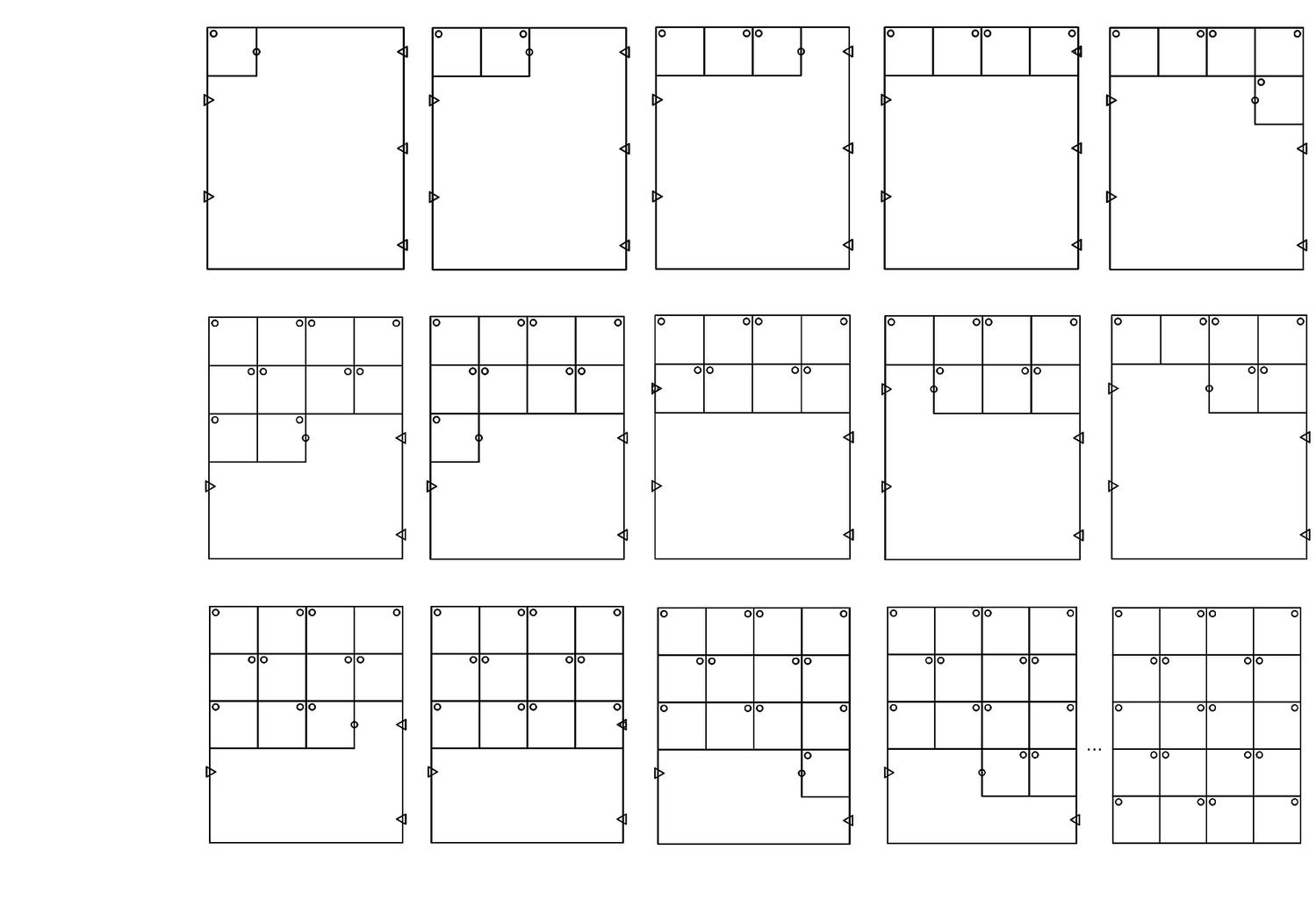
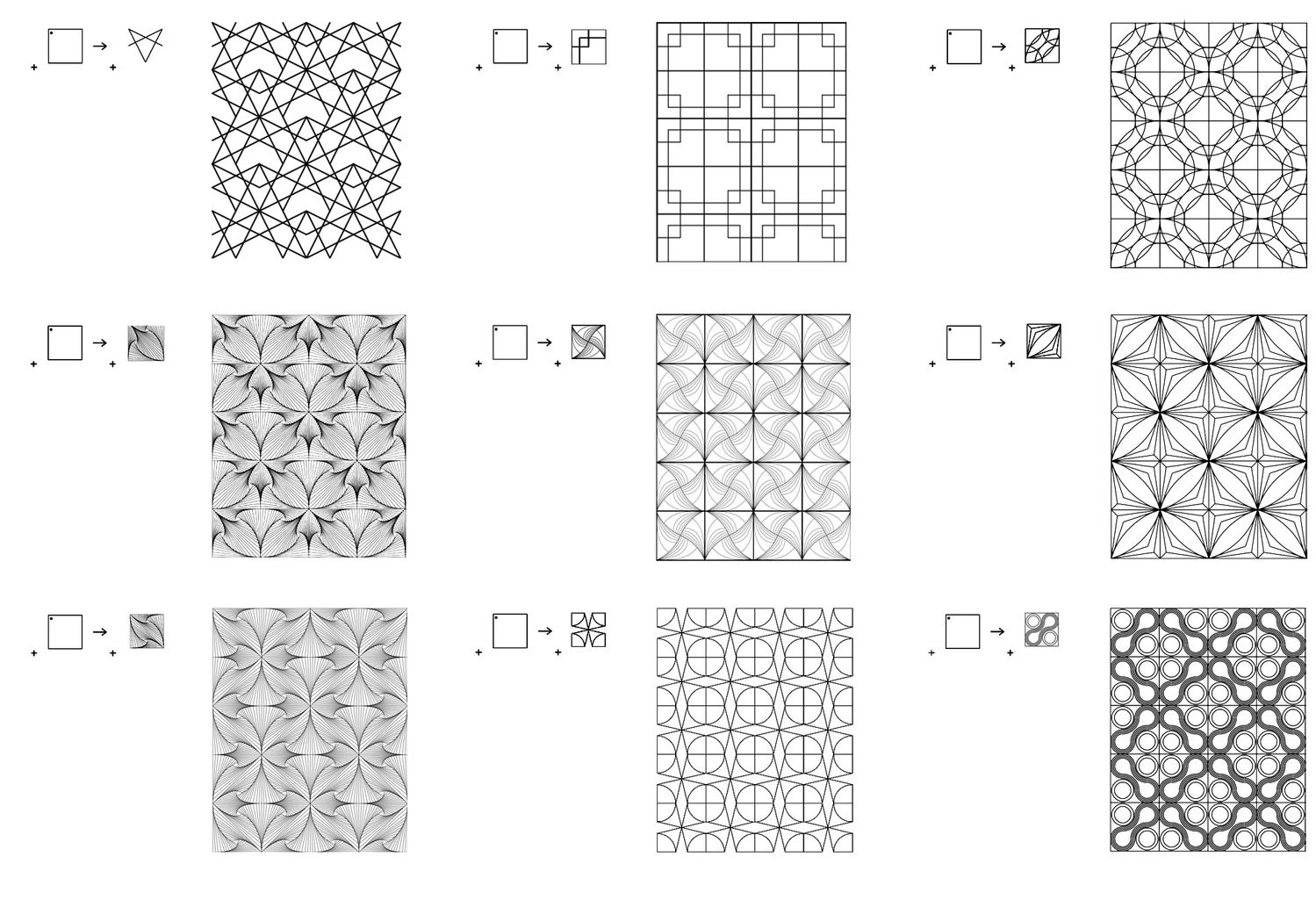
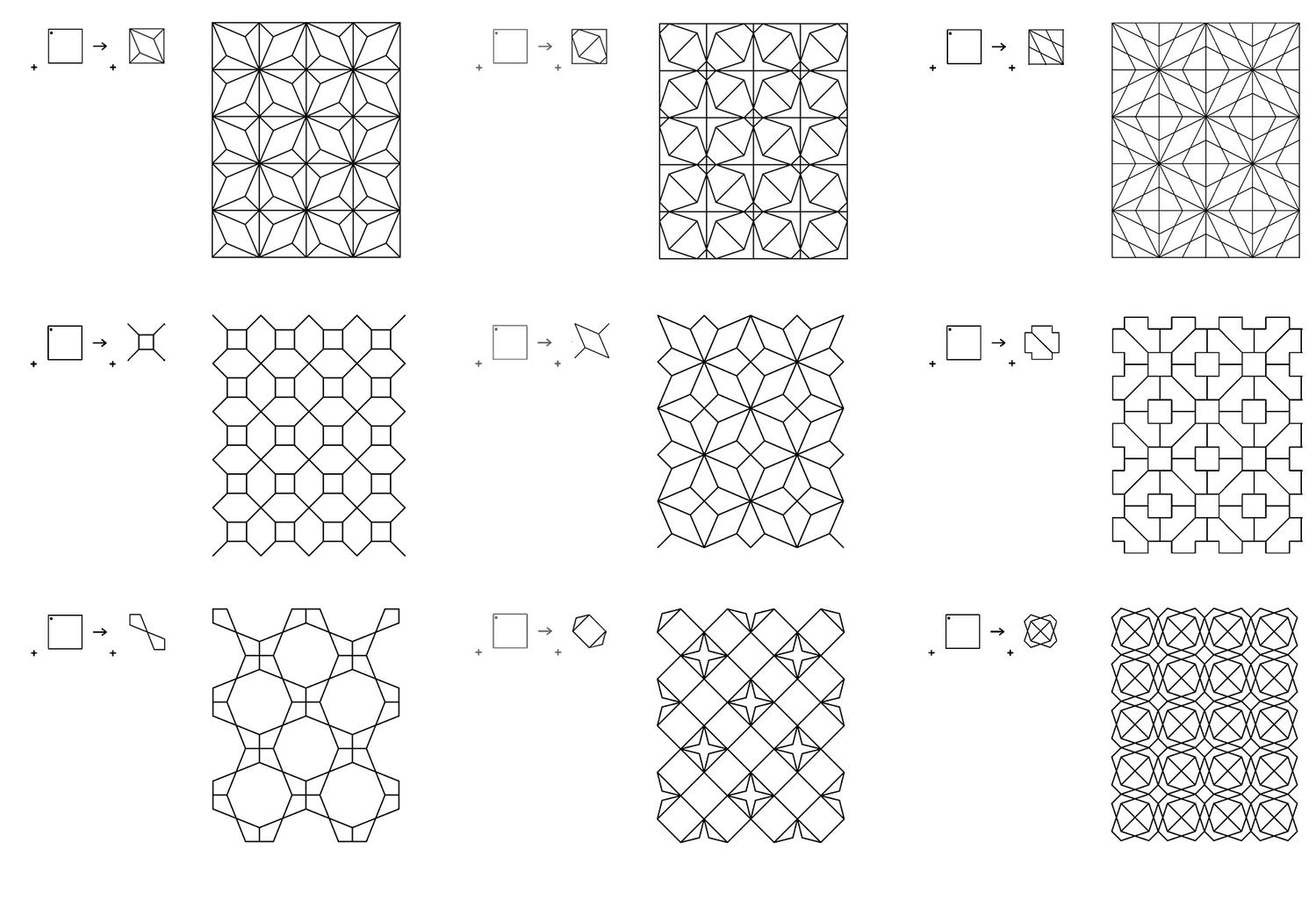
The very same parts combine one with another to create a visually staggering world rising from the singularity of the 1-line shape, to the 8 2-line shapes, to the 519 3-line shapes (among which there is the triangle and its parametric variations) and to the 317,065 4-line shapes (among which there is the square and its parametric variations). Checking these numbers, it is easy to see that any parametric shape consisting of 4 lines or strokes in the plane is an instance of the 317.593 possible 4-line shapes. The numbers for larger sets of lines increase dramatically to further the key insight of the formalism on a unique description of any shape out there.
The algebraic calculations of figure inventories for up to 4-lines so far are done in Mathematica. The calculation of the chirotopes for the underlying matroids are done by hand. The specification of the shapes is modeled in Grasshopper and visualized in Rhino. The project has been carried through with substantial help from Cvetelina Hill, May Cai and Nicholas Liao, doctorate and undergraduate students, respectively, at the School of Mathematics, College of Sciences at Georgia Tech.
Threeness
Athanassios Economou, Josephine Yu and James Park
2018
Keywords: Lines; Shape grammars; Burnside' s lemma; Polya's theorem of counting
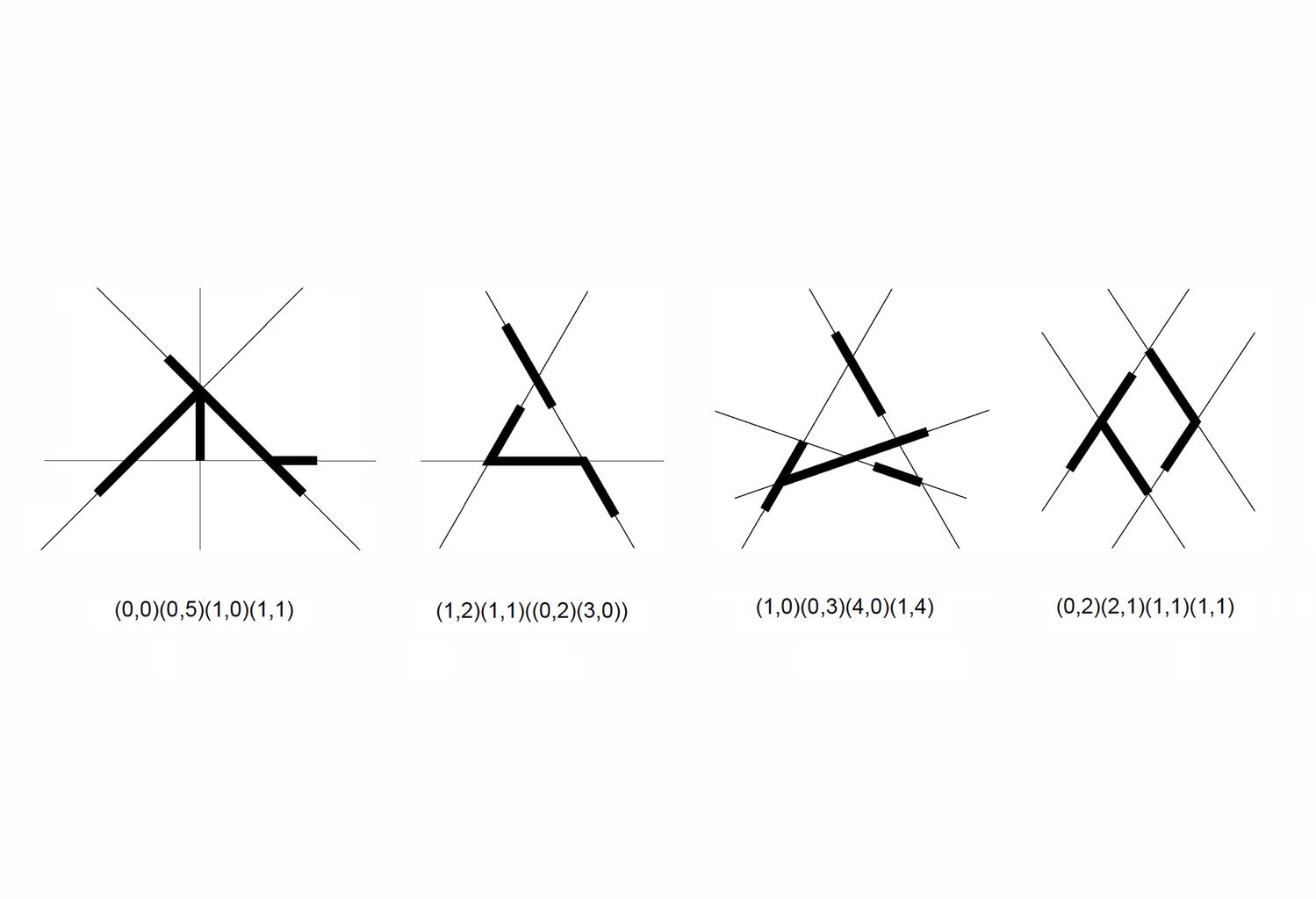
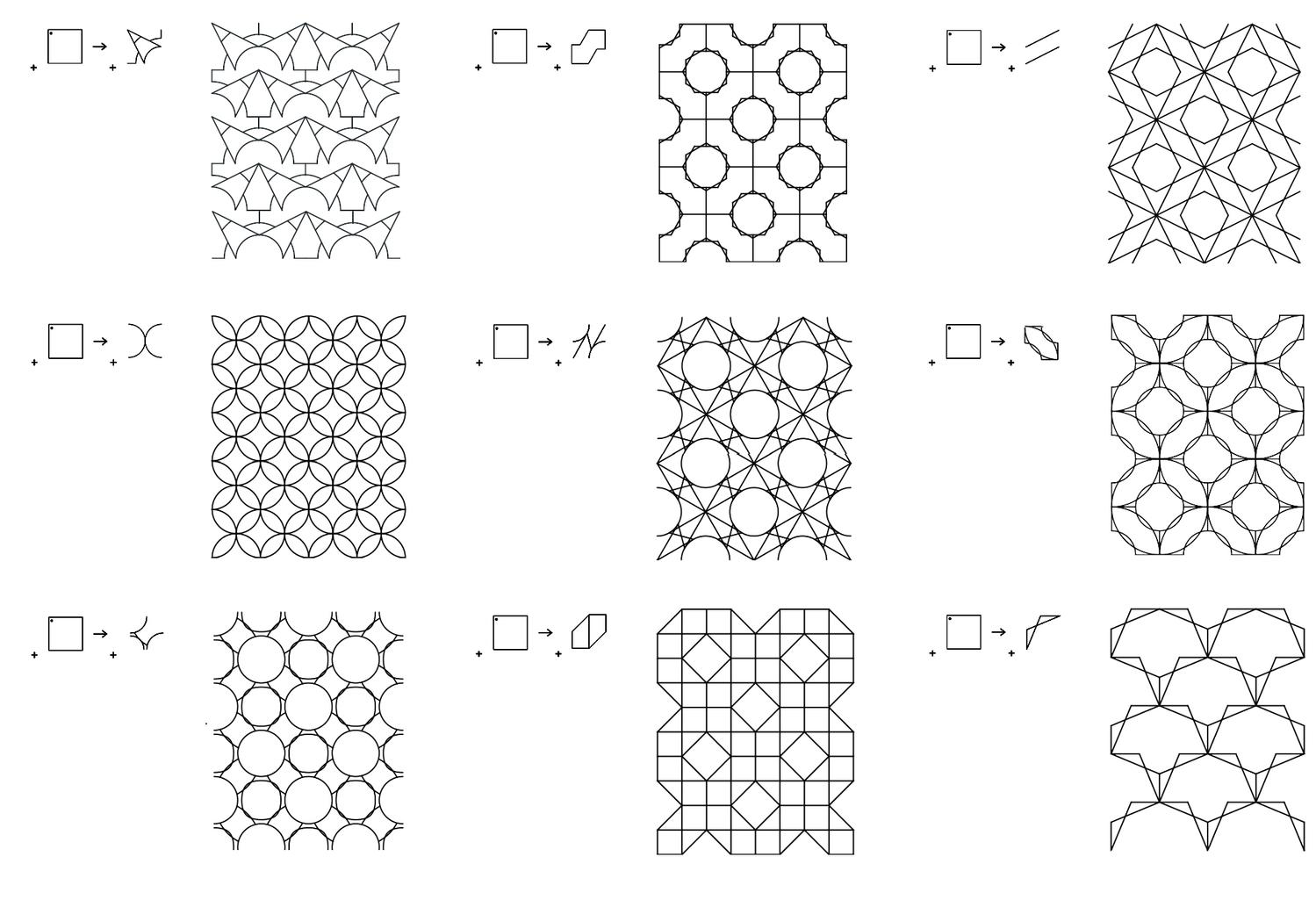
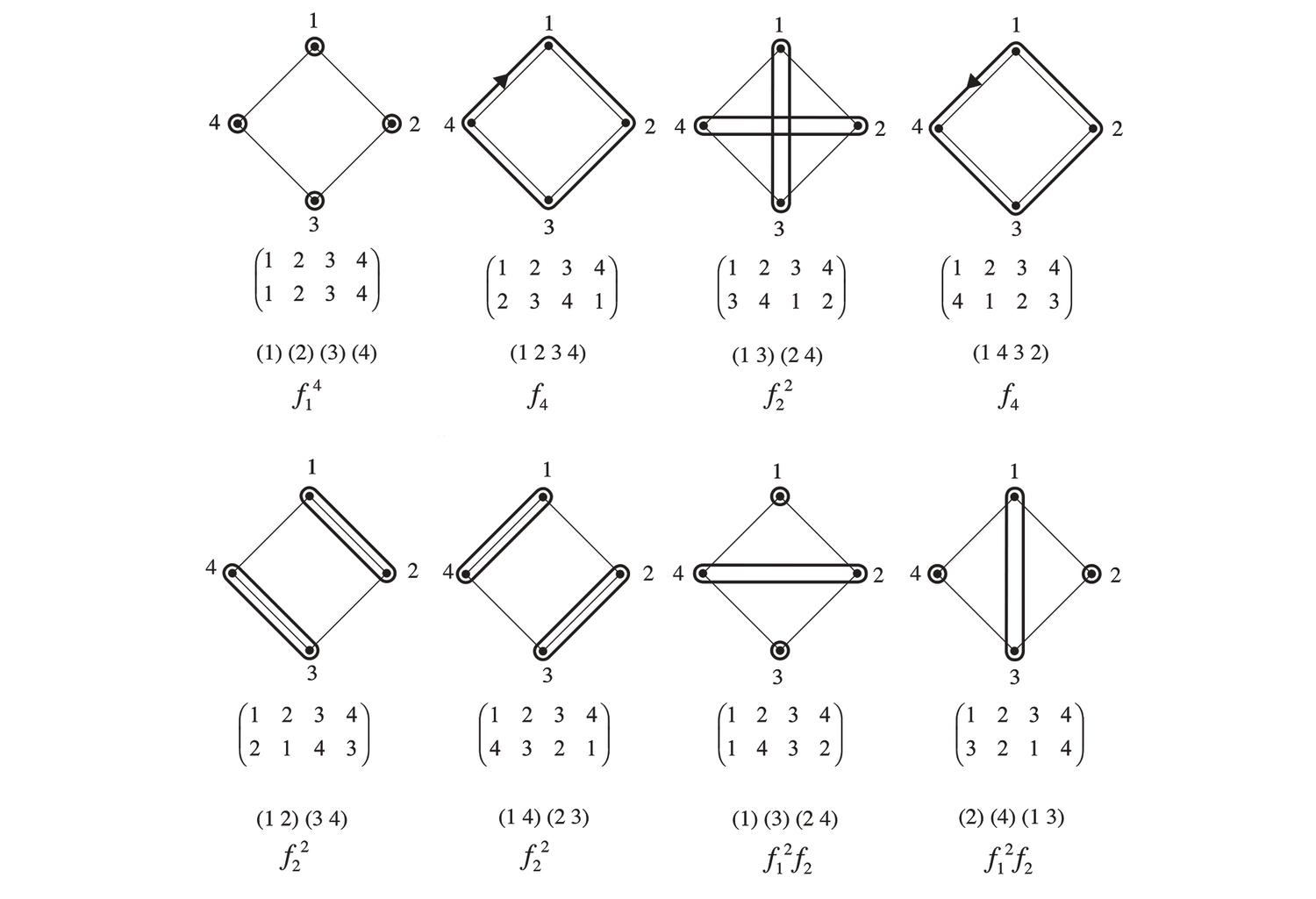
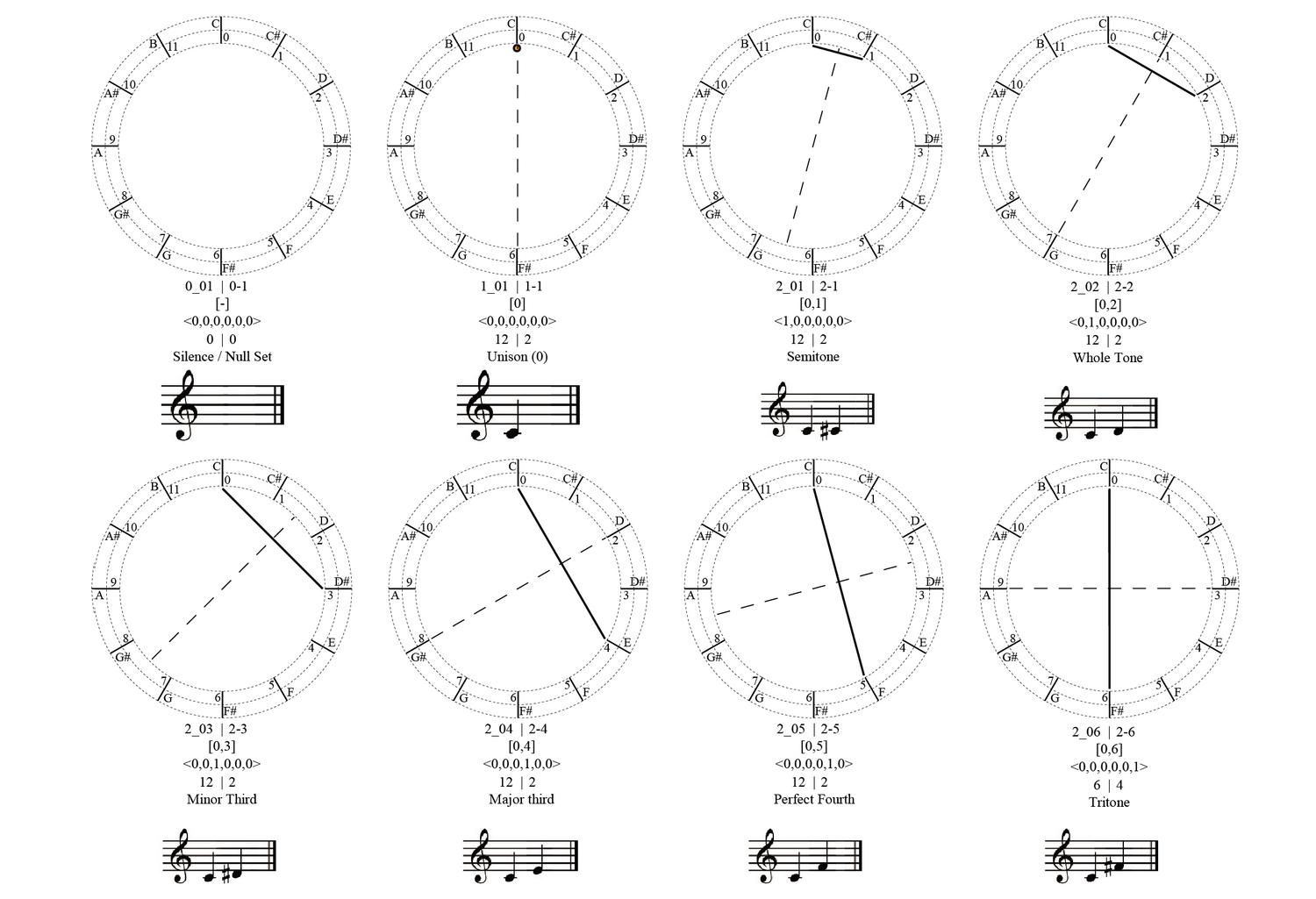
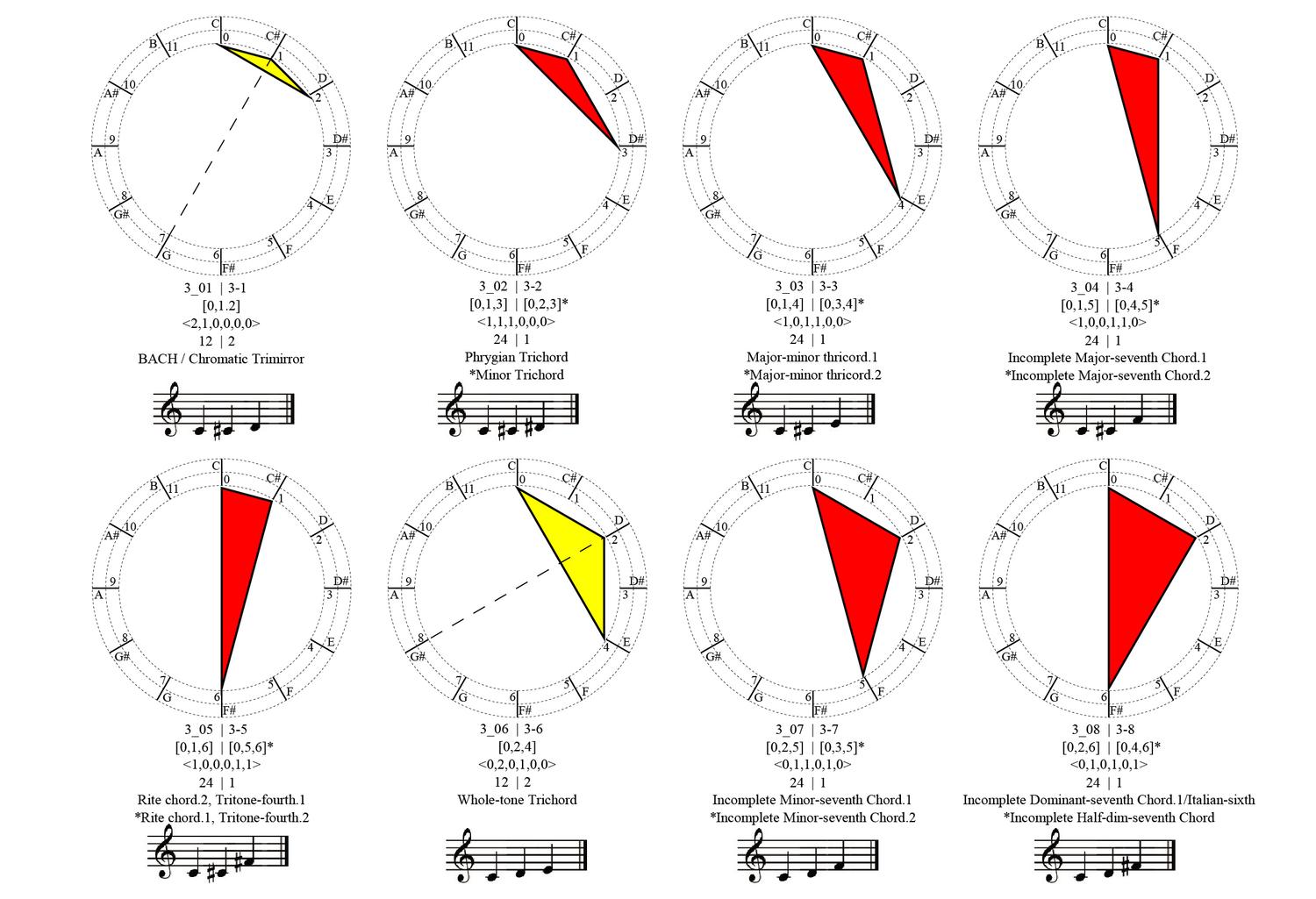
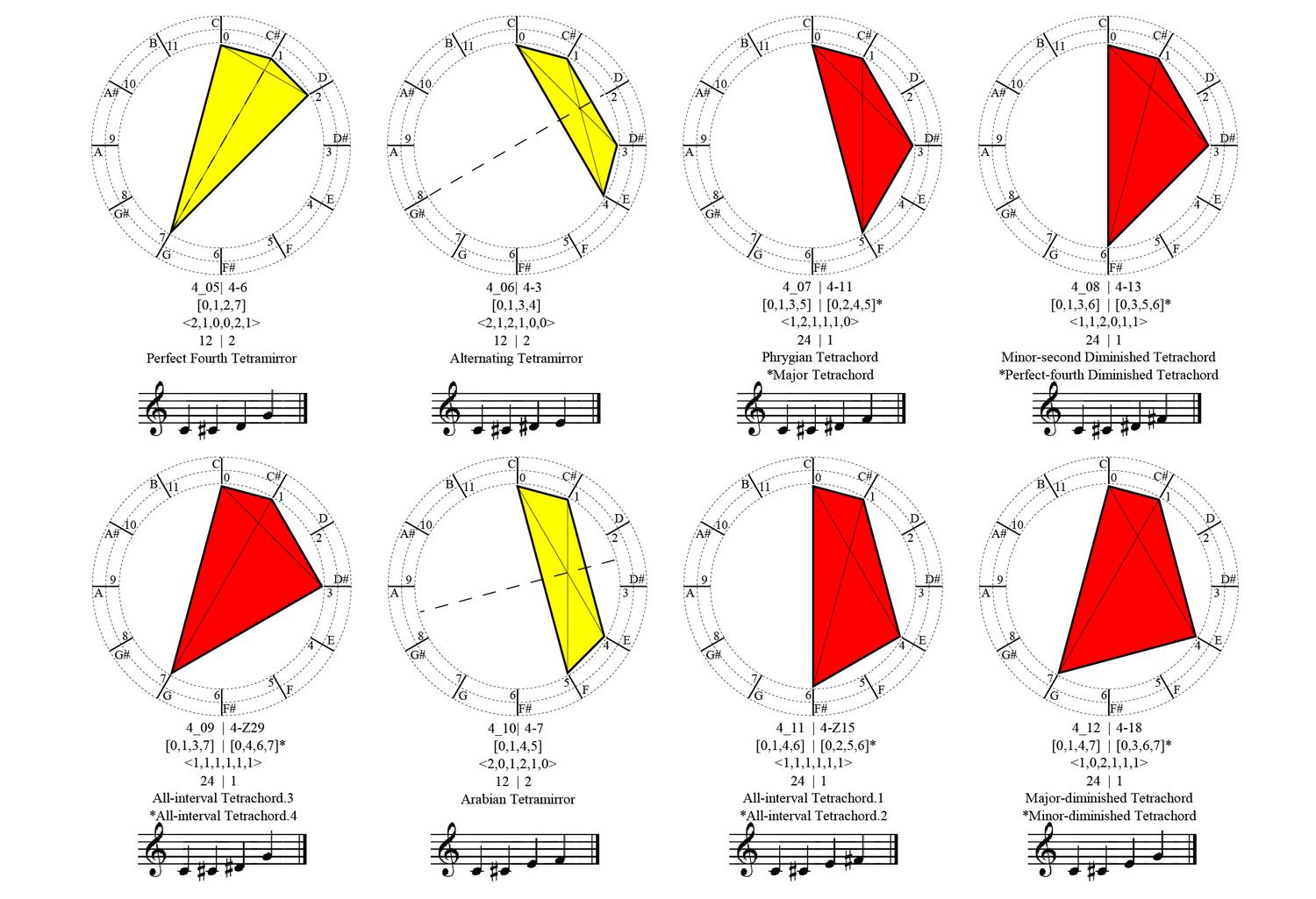
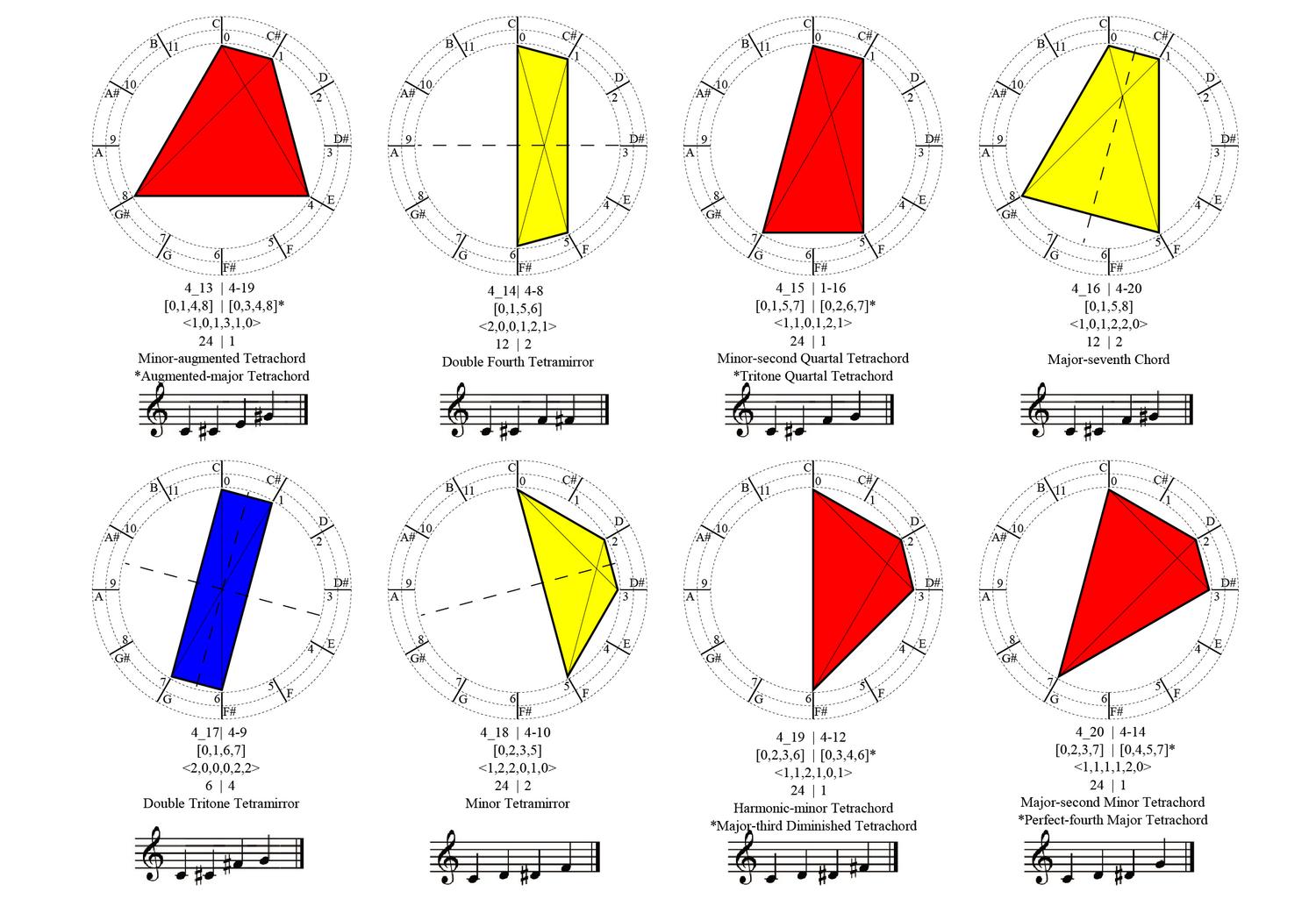
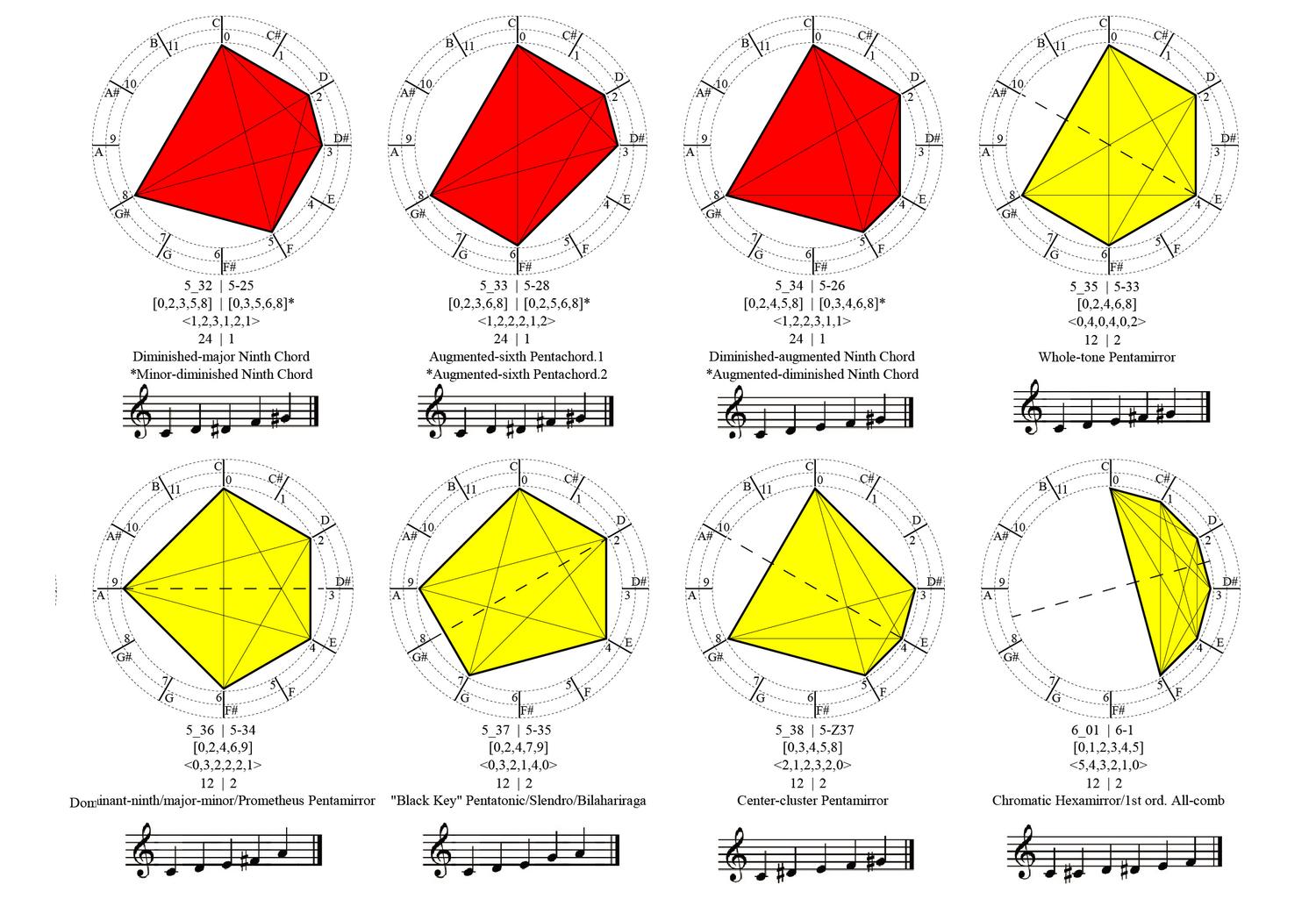
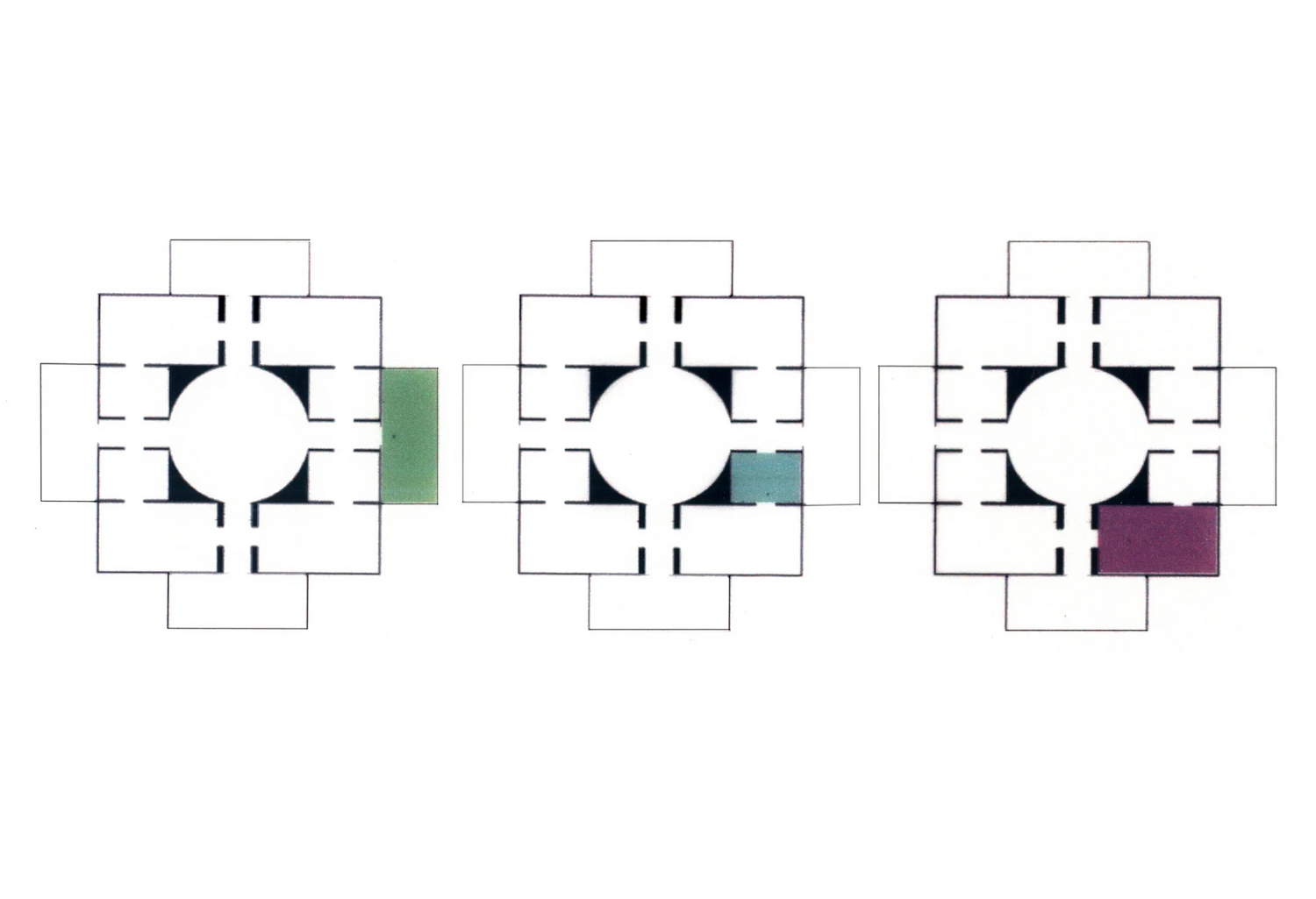
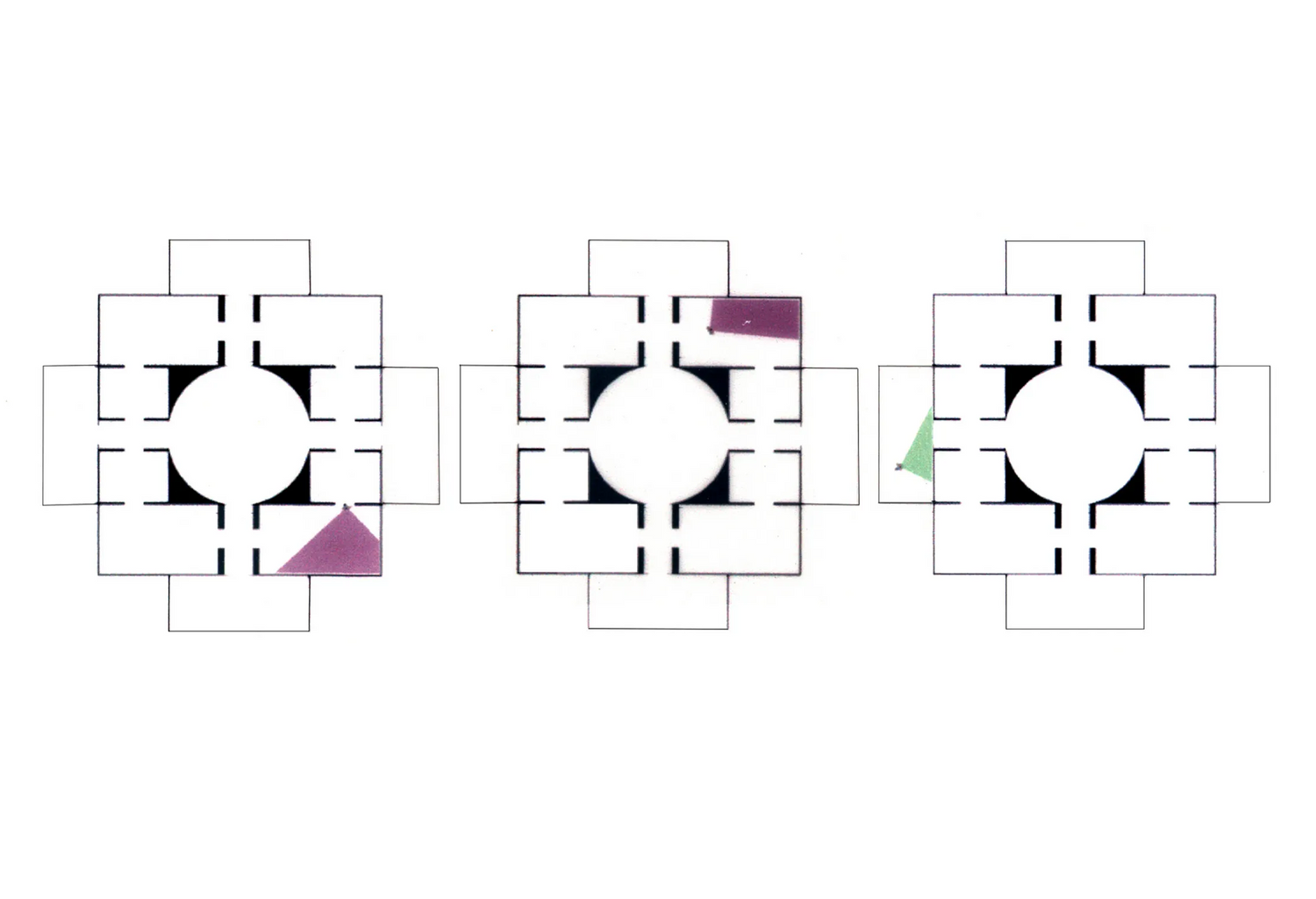
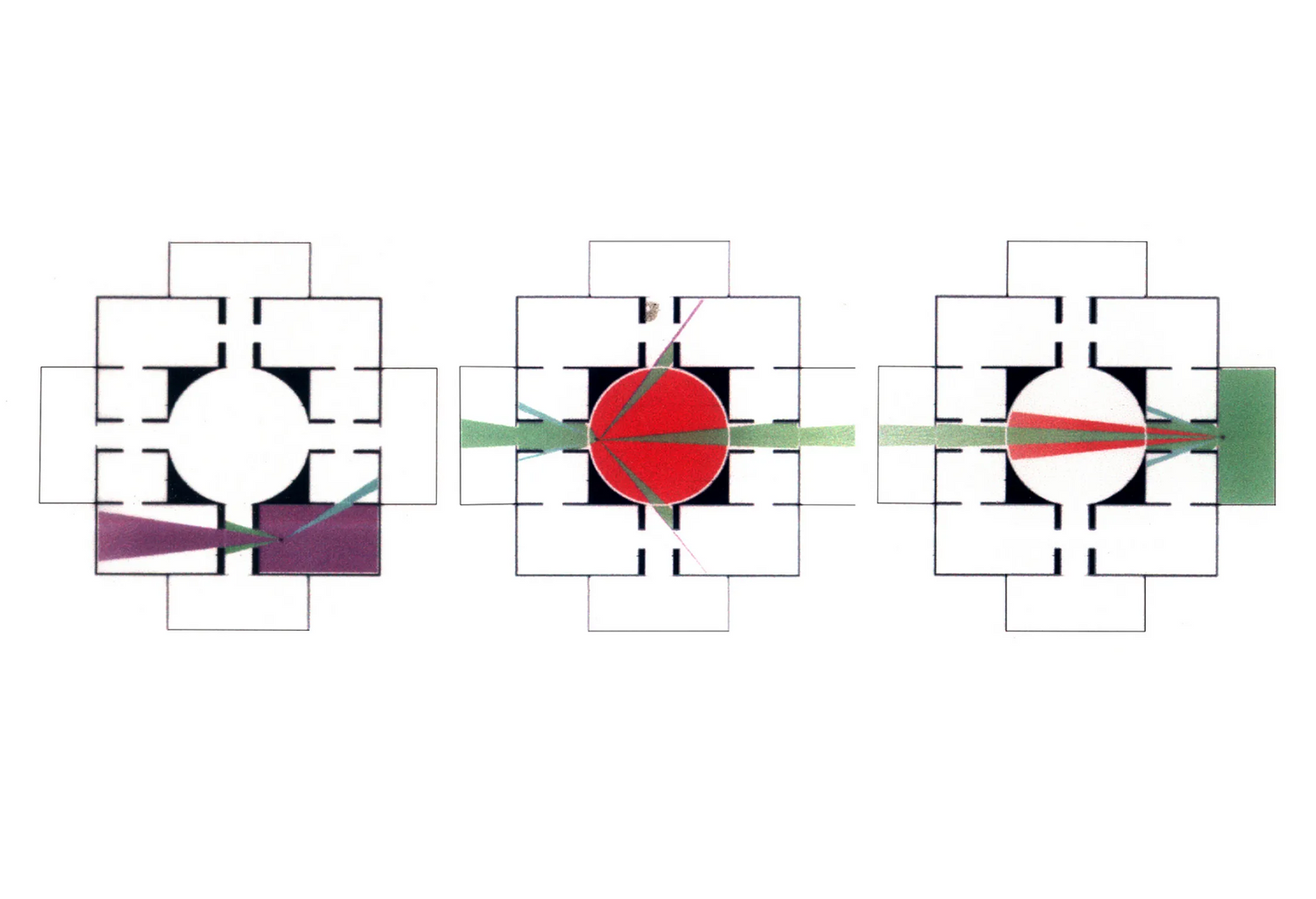
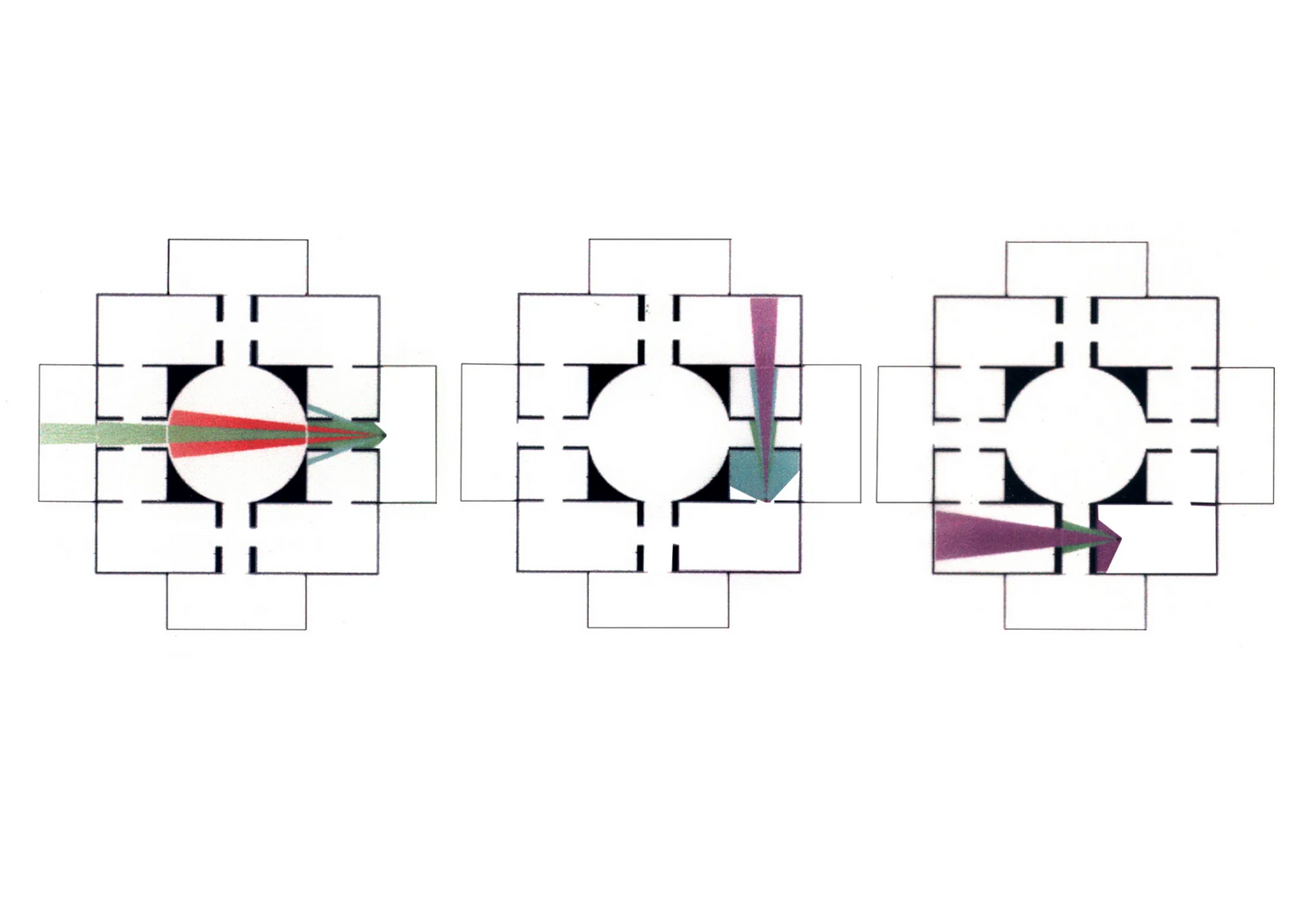
We all can recognize simple shapes and relations effortlessly, for example, triangles of all sorts, no matter their specific geometric characteristics, be them scalene, equilateral, isosceles, Pythagorean, 30-60-90, or what-have-you. After all, all triangles consist of three lines (edges) connected in three points (vertices). Still, if someone asks the question about how many shapes can be made from three straight line segments that may be connected to one another or not, intersecting one another or not, floating to another or not, the answer is not straightforward. An unambiguous way to classify, retrieve and instantiate 3–, 4–, 5–, 6– and more generally, n-line arrangements to construct shapes will potentially have a great impact in computer shape recognition and CAD applications. The complete calculation of all possible parametric shapes made of 3 lines is given below without counting parallelism and/or intersections of valency greater than 2. All 390 shapes are unique, or otherwise, non-equivalent with respect to the symmetry group of the triangle, that is, there is no symmetry transformation of the Euclidean plane that can map one configuration to another.
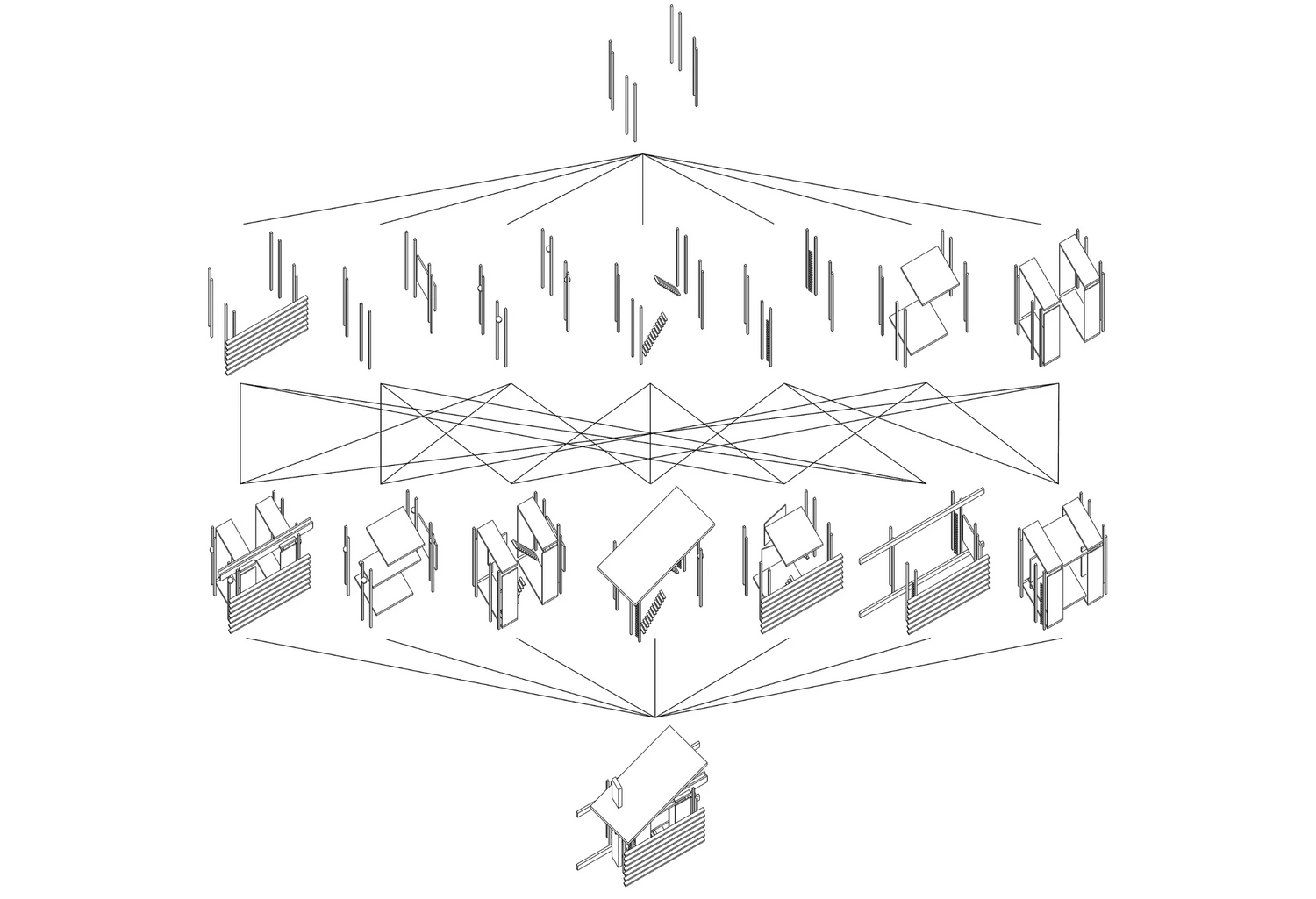
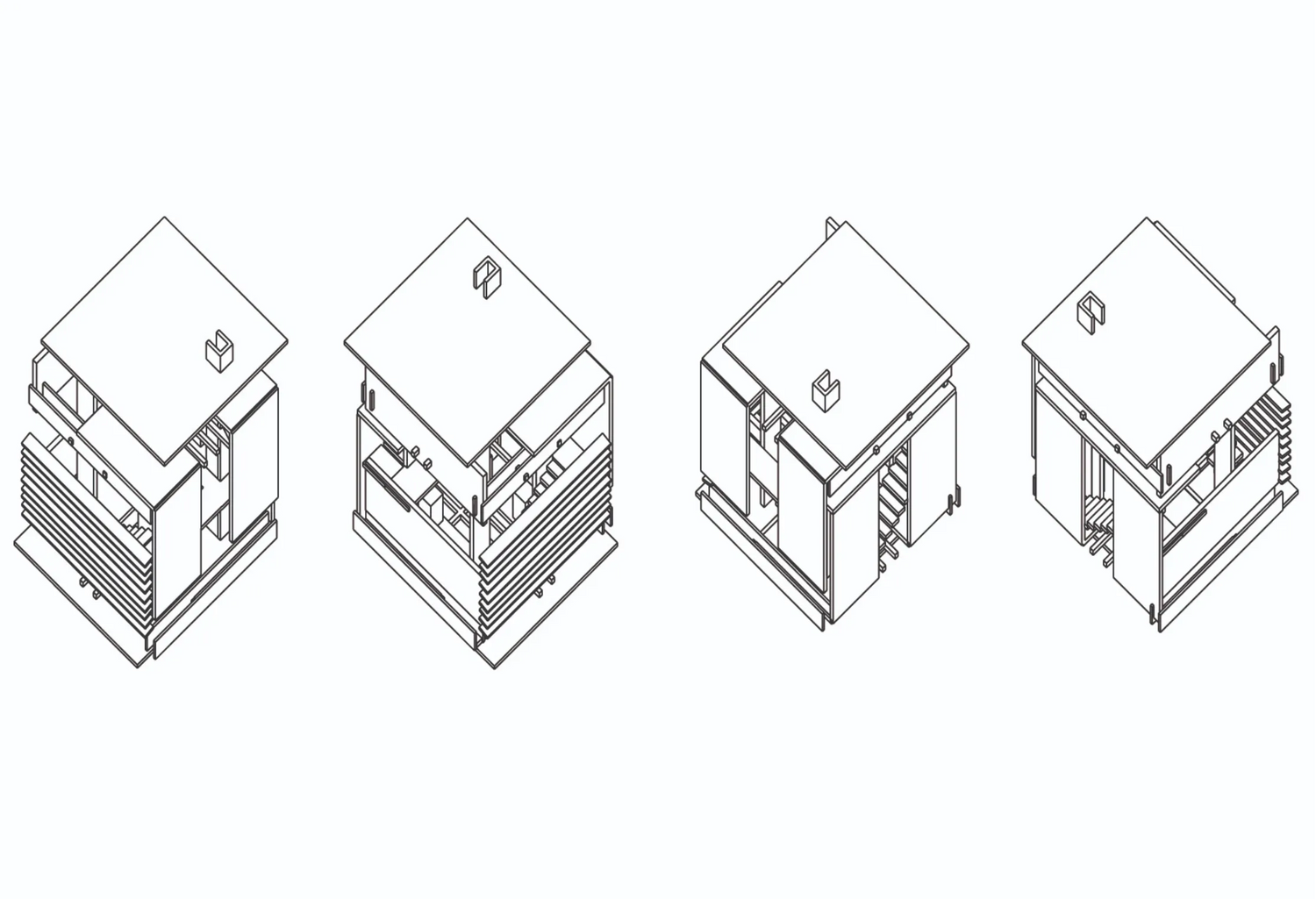
Ice-ray Tilings
Athanassios Economou and Kurt Hong
2018
Keywords: Shape machine; Shape grammars; Visual programming; Algorithmic composition; Ice-rays
In 1949 Daniel Dye published his book A Grammar of Chinese lattice showcasing an influential catalogue of Chinese ornamental and grilled window designs ranging from the 10th c. to the 19th c. Some of the designs published in the book were reworked by George Stiny during the '70s in his paper Ice-ray: A note on the generation of Chinese lattice designs, to showcase his new theoretical method to approach design in terms of visual rules that apply recursively to generate designs.
This work takes on Stiny's grammar of an 18th c window design at Chengtu, Szechwan, one of the two rule-based compositional methods outlined in the paper, and puts it into practice as an introductory exercise in the shape grammar class at Georgia Tech. The grammar was implemented individually by each student using the shape machine, the shape grammar interpreter of SCL in Rhino, and transformed appropriately as needed. The deliverables of the study are a series of new designs implementing different motifs and compositional ideas to transform the rule 6 of the original grammar. Significantly, all different motifs tried by the students were drawn directly within the modeling environment of Rhino showcasing a truly visual programming environment for spatial design. Acknowledgments: We want to thank Nunggu Ahn, Zeinab Babalou, TJ Bogan, Yousef Bousehri, Warren Campbell, Vincent Chang, Alexander Clegg, Fatima Javeed, Zachary Lancaster, Andressa Martinez, Amelia Mclean, Eri Natsumi, Victoria Olaogun and Yuqin Zhong for their enthusiasm and hard work during the project.
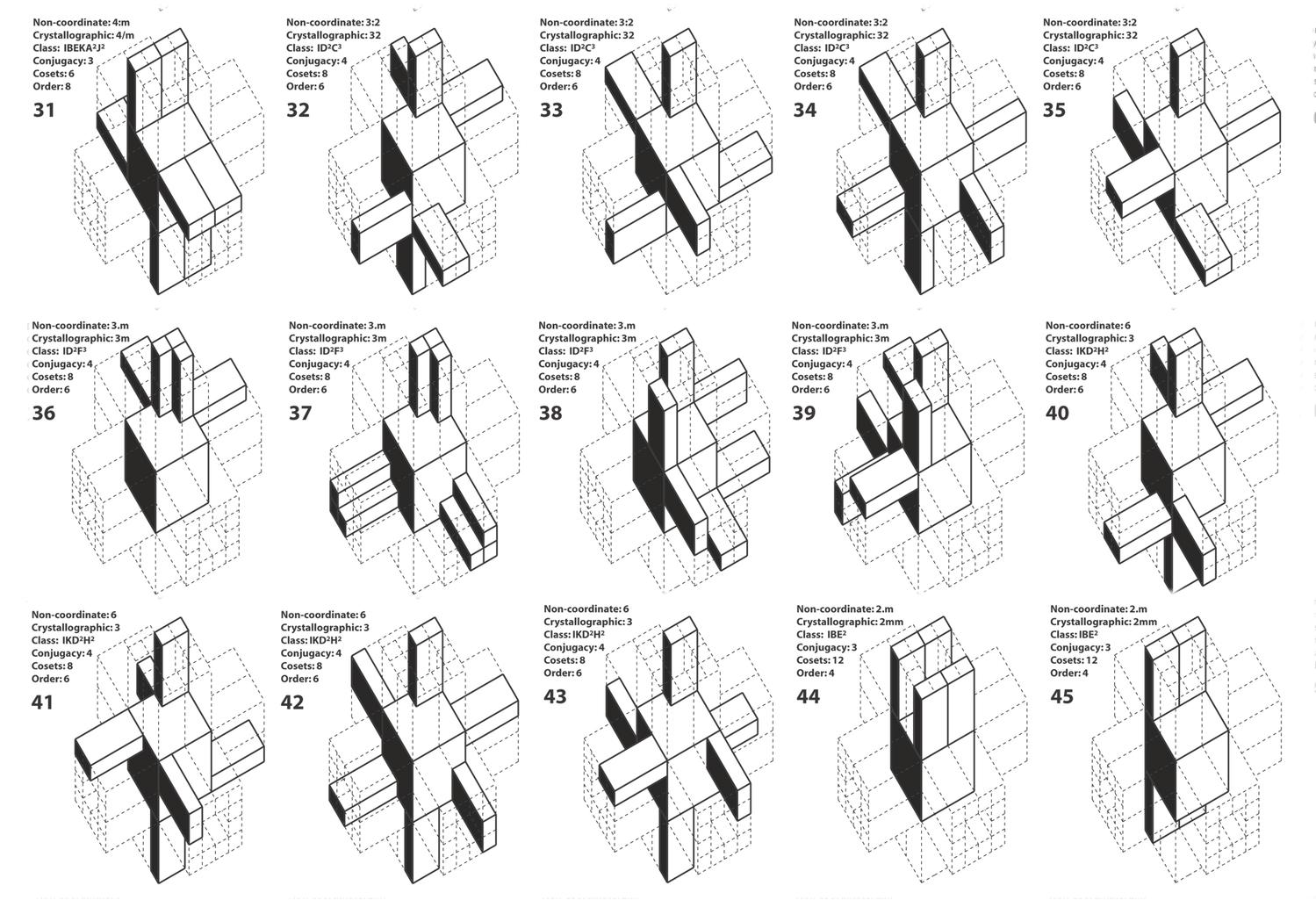
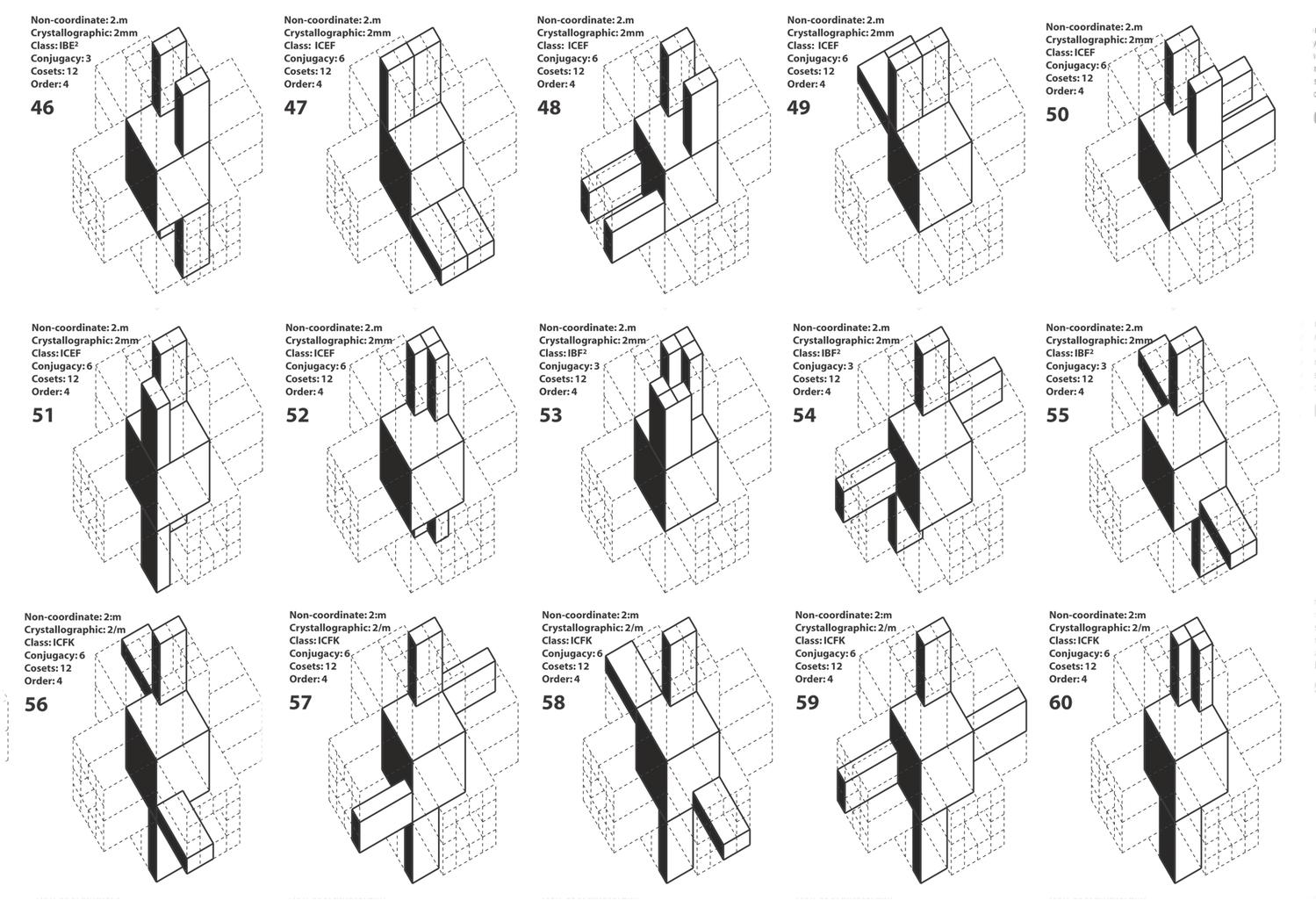
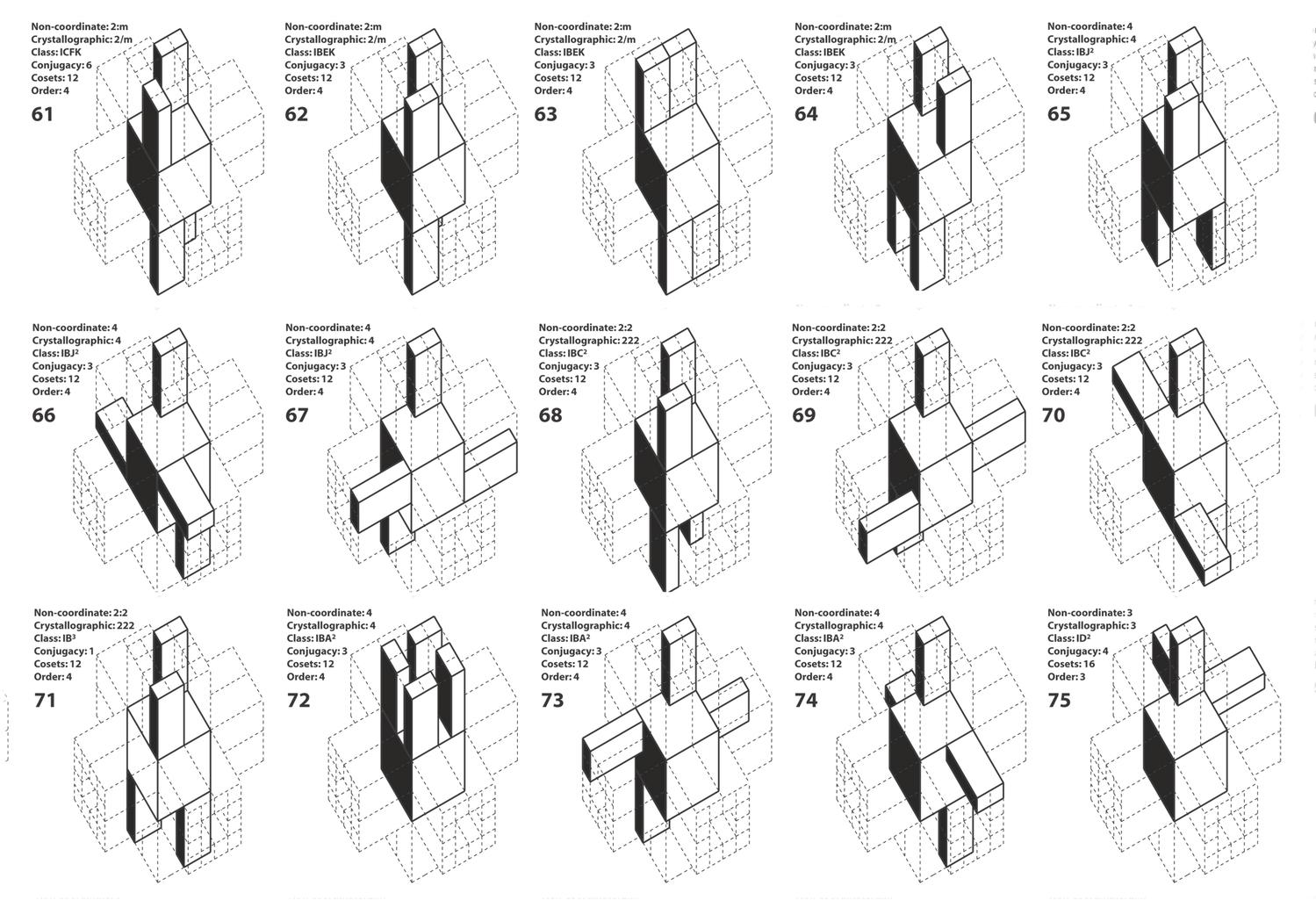
n-Dipyramids
Athanassios Economou and Thomas Grasl
2017
Keywords: Configuration; Perfect coloring; Polya’s theorem of counting; Sieves, Xenakis; Counterpoint; Rhythm
The sieve is a powerful formal tool developed by the composer / architect Ioannis Xenakis to create integer-sequence generators that can be used for the generation of various numerical patterns to represent pitch scales, rhythm sequences, loudness progressions, density patterns, timber systems and so forth, The decomposition of a n-modulus of the sieve can be modeled as the arrangement of 2 colors x and y upon the faces of a regular n-polygon whereas the color x represents the sieve content and the color y represents the numerical distance between the sieve content.
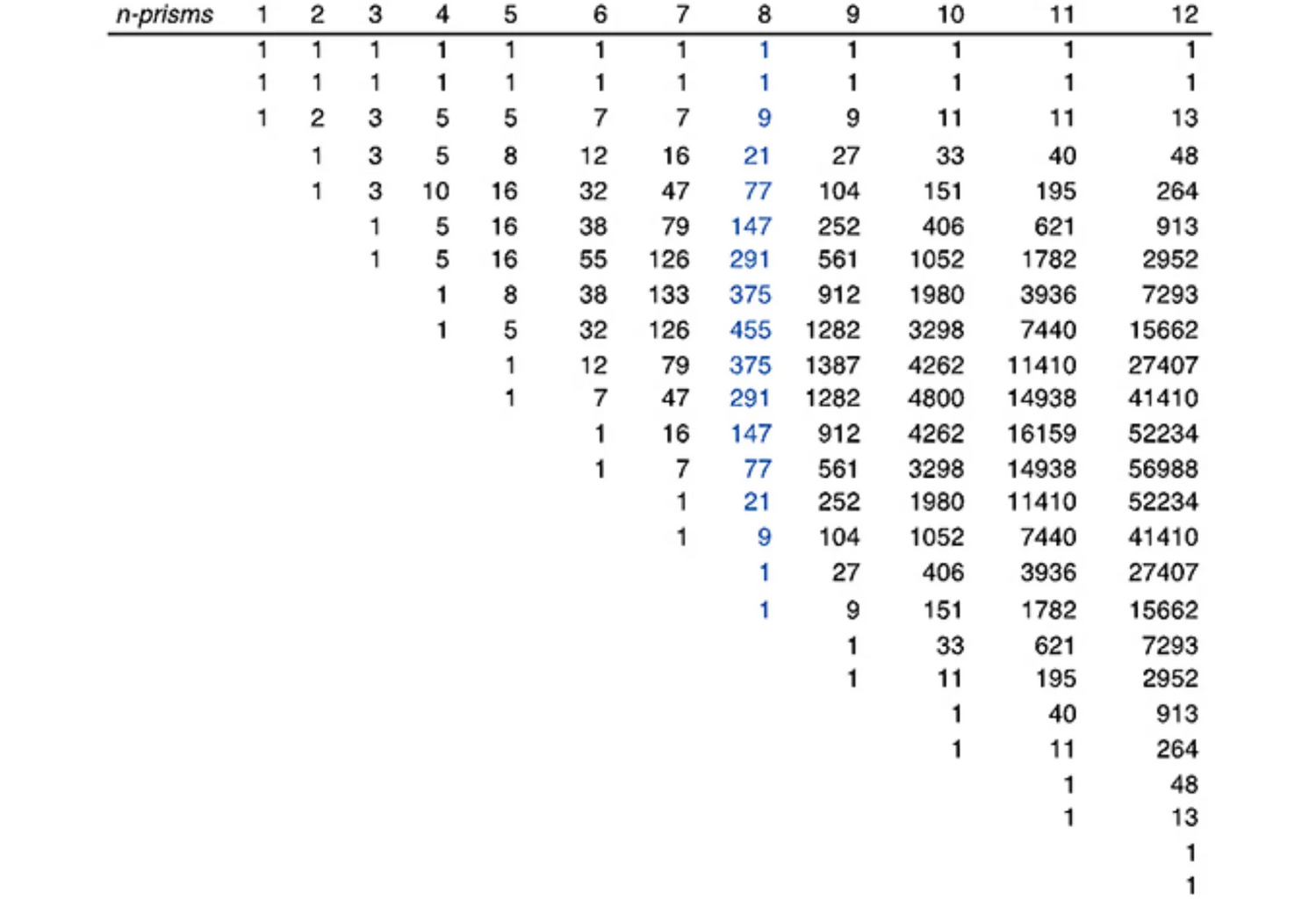
Here, the work extends the model to capture spatial relations between sieves. The key idea to extend the model is to look at the possible spatial relations between sieves in Euclidean space and primarily in three-dimensional space. The candidate shapes to capture the notion of decomposition of a module are the extensions of the regular n-polygons in the Euclidean plane to the regular prisms in Euclidean space, and even more so, the regular n-dipyramids, the duals of the regular n-prisms. The computation here gives the complete number of all colorings of the faces of 12-dipyramids for up to 5 colors and the emphasis is given in the calculation of 2 colors as the three-dimensional extension of the model for the enumeration of the sieves wrapped around 2 n-polygons in space. More specifically it can be shown that there are 2 ways to color the 2 faces of an 1-dipyramid with 1 color, 6 ways to paint the 4 faces of a 2-dipyramid with 2 colors, 13 ways to paint the 6 faces of a 3-dipyramid with 2 colors, 34 ways to paint the 8 faces of the 4-dipyramid with 2 colors and so forth. The computation here foregrounds the calculation of the coloring of the 16 faces of the 8-dipyramid because this shape presents all possible symmetries found in the 7 infinite families of three-dimensional regular prisms. More specifically, the table shows that 16 faces of an 8-dipyramid can be painted with 2 colors in 2299 distinct ways. In a similar manner there are 2299 polyrhythms that consist of two rhythms played one against the other.
Sieves
Athanassios Economou and Thomas Grasl
2012
Keywords: Sieves; Xenakis; Group theory; Symmetry; Enumeration
The sieve is a powerful formal tool developed by Xenakis to create integer-sequence generators that can be used for the generation of various numerical patterns to represent pitch scales, rhythm sequences, as well as patterns of loudness, density, timber and so forth (1). Xenakis used the sieves in a series of musical and architectural works (2), (3), (4)
The key motivation for the work outlined here is to capture and visualize the properties of the algebra of the sieves looking at the decomposition of the moduli that emerge out of the combination of the sieves. Xenakis asserted that his algebra of sieves revealed insights into fundamental aspects of composition. Here these hidden symmetries are identified and foregrounded for any modulus however complex.
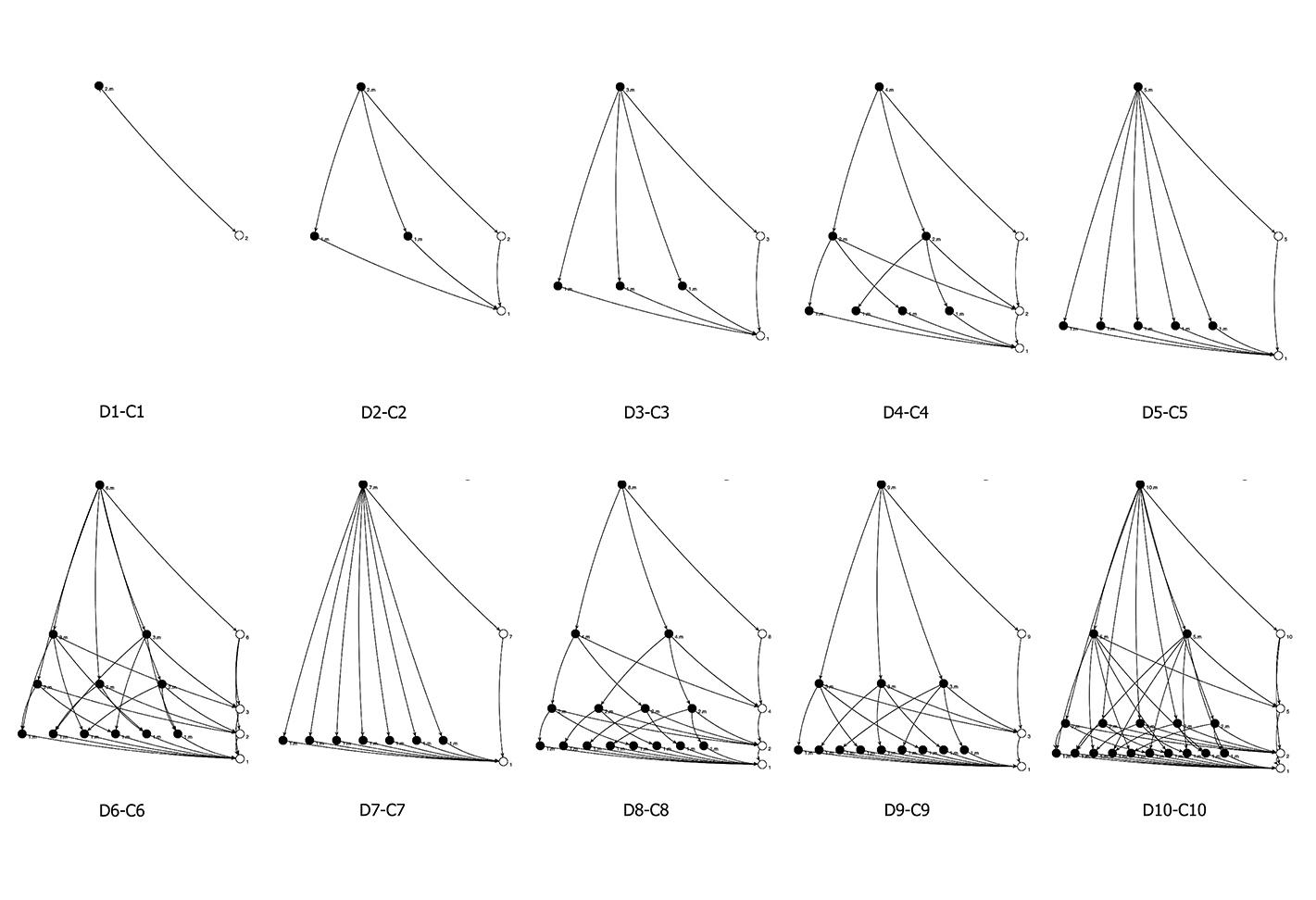
The formal tools for the inquiry on sieves are taken from Lagrange’s theorem on subgroups of given order and Polya’s theorem of counting non-equivalent configurations with respect to a given permutation group. Here the theorems are applied within an automated computational framework that automatically generates all the symmetry subgroups of a given symmetry group (5), calculates the cyclic index of all symmetry groups and subgroups of any finite shape (6), computes the figure inventory of any number of variables upon the cycle index (7), produces patches showing the data flow of the moduli (8) and visualizes the result of all non-equivalent configurations with corresponding isomorphic two-dimensional subshapes of regular n-gons (9). The project, background, framework and formal details are given in (10).
Subsymmetry Lattices
Athanassios Economou and Thomas Grasl
2009
Keywords: Polya’s theorem of counting; Symmetry; Point groups; Graphs; Fruchterman-Reingold algorithm; Rhythm
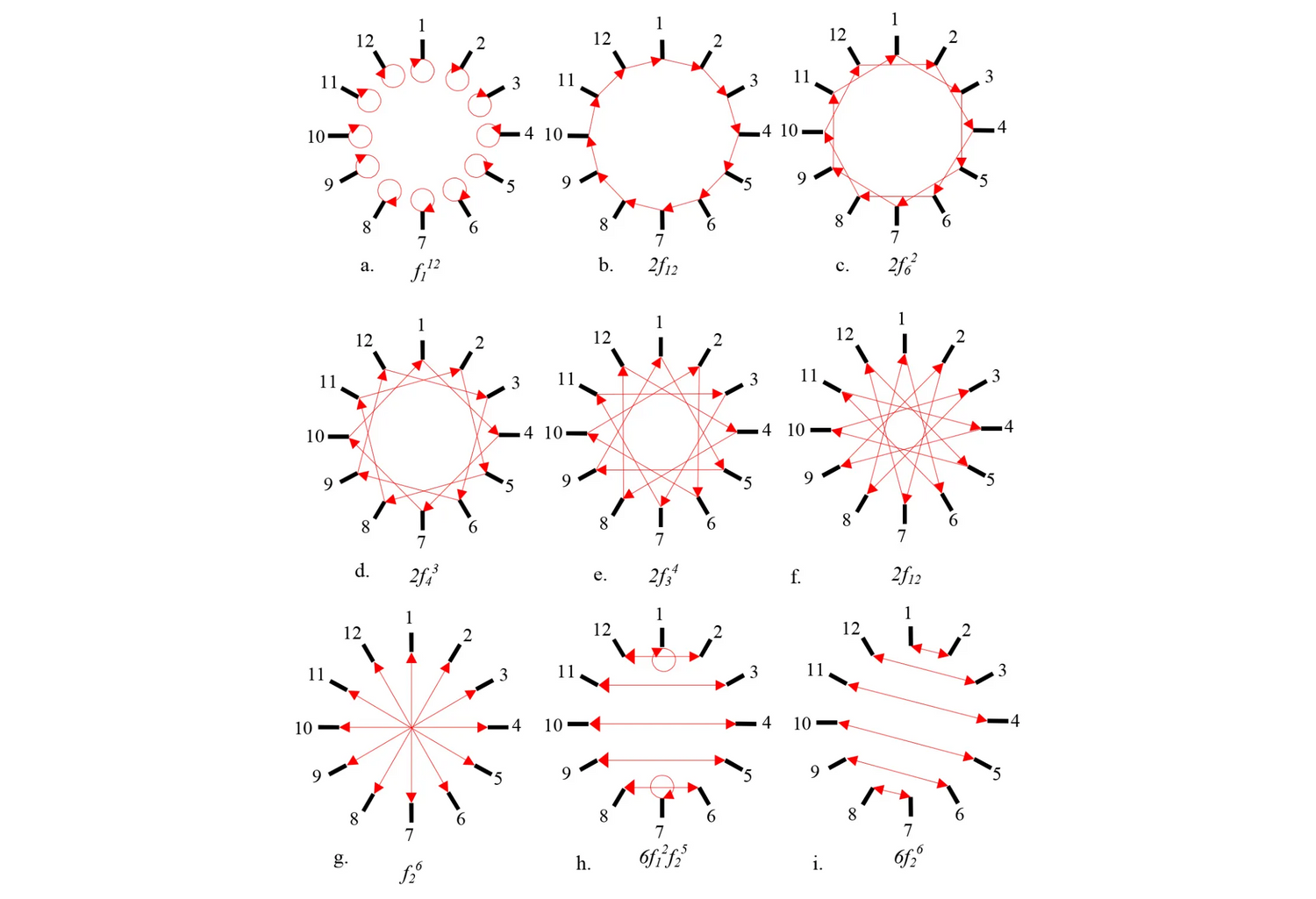
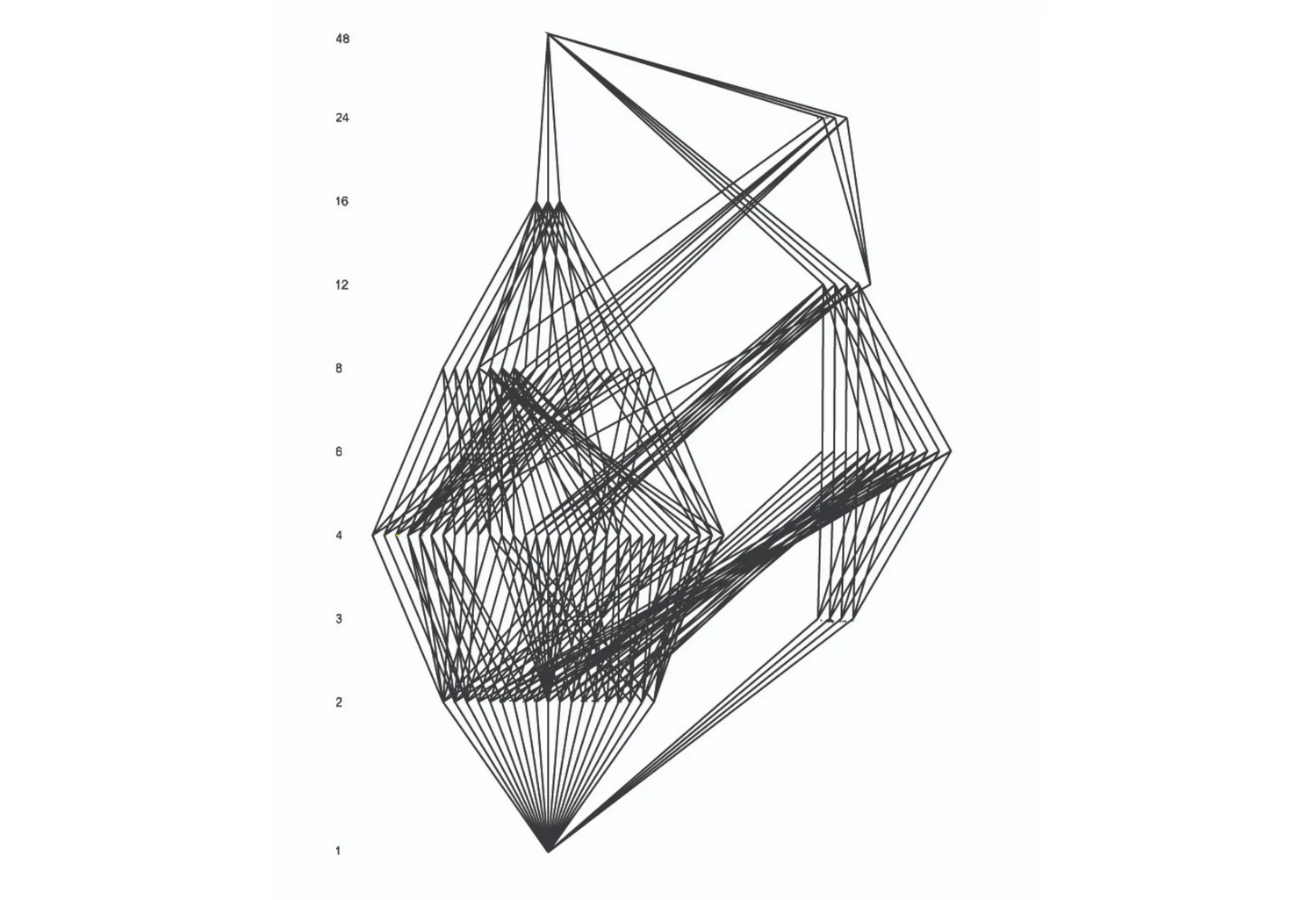
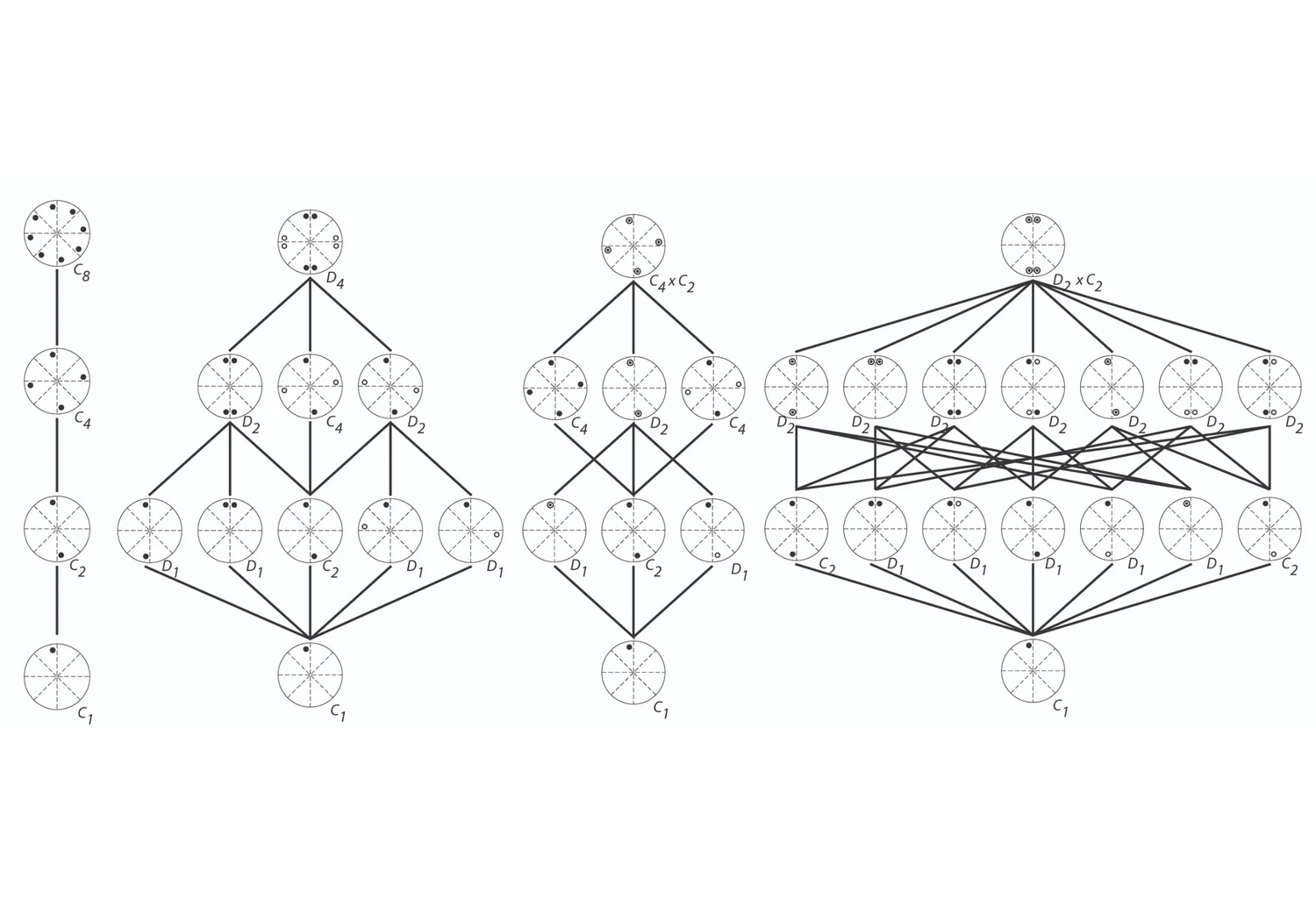
One of the most interesting aspects of symmetry theory and pattern analysis and composition is the part relation (<) of symmetry groups; the elaborate and complex hierarchies of symmetry groups and subgroups, all nested one within the other, point to their direct correspondence with complex compositional structures of spatial patterns and suggest a precise methodology for formal analysis and composition in architectural design. This work looks closely at a specific set of symmetry groups - the two infinite types of the planar groups, the cyclic and the dihedral ones - and provides an automated environment to enumerate and represent the subgroups and their relationships with lattices in a graph theoretic manner. The complexity of these structures can be astonishing and it is suggested here that its graph theoretical representation can contribute to a better understanding of problems of spatial complexity in architectural design. The computational approach outlined in this work may indeed be used in formal analysis to identify all spatial repetitions and spatial correspondences that can be observed in a design. Alternatively, the approach may be used in formal composition to structure the design choices and bring to the foreground the whole range of spatial relationships available to the designer at any level of the design inquiry.
The computation and manual illustration of all possible subgroups for a given group n is not a trivial task; the theory for the computation here relies on a sorting based on two theorems proved by Lagrange and Sylow respectively: Lagrange theorem identifies a very precise numerical relationship between subgroups and groups, namely that the order of a subgroup always divides the order of a group; Sylow's theorem proposes that if a number h is a power of a prime and divides the order of a group, then the group has a subgroup of order h. Here the automation relies to a routine to generate the complete list of all prime factors for a given number n. The simplest, albeit not most efficient, algorithm to generate the primes is the sieve of Eratosthenes. Since computing time is not a key feature for the relatively small magnitudes dealt in this project, algorithmic simplicity has been chosen over efficiency. Once the primes are extracted all possible distinct products are computed and tested to produce the possible lists of factors and the corresponding cyclic and dihedral subgroups. The generation of the graphs is then a straightforward task of iterating through the factors and generating the n/f nodes noting each time which set of operations the node represents.
The completion of the illustration of the structure of the graph is done with the pictorial representation of the edges of the graph deduced from each label and iterating over the nodes. The pictorial representation of the graphs is given in two ways: The first representation shows all possible subgroups and maps all possible relationships between them; this representation offers the most detailed view in the inner structure of any design and illustrates nicely the stunning complexity found even in the simplest of structures. The second representation foregrounds the qualitative difference between rotational and reflective symmetries and classifies all subgroups and their relations in terms of two distinct classes, the cyclic and the dihedral groups respectively; this representation relies on a specific construct from group theory, the construal of conjugacy or equivalence relationships for elements of the group and essentially produces graphs where all identical instances of a dihedral group of some order n are collapsed to a single node; this preserves the relations between the various subgroups and produces a leaner graph. The application uses the Fruchterman-Reingold algorithm for the collapsed representation of the graphs.
Soundshapes
Athanassios Economou
2006
Keywords: Cube; Hexahedral group; Permutation groups; Cycle index; Symmetry; Configuration;
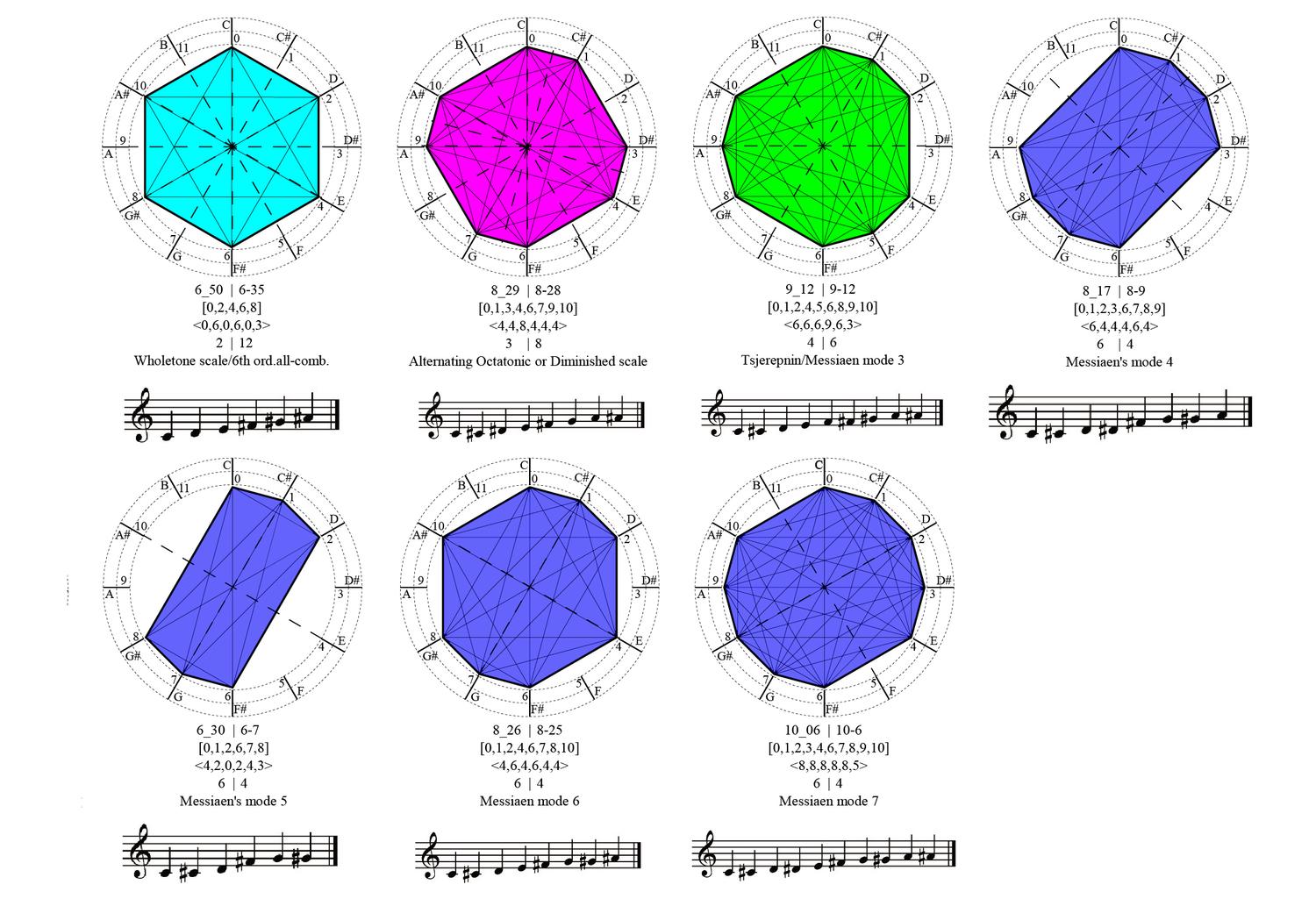
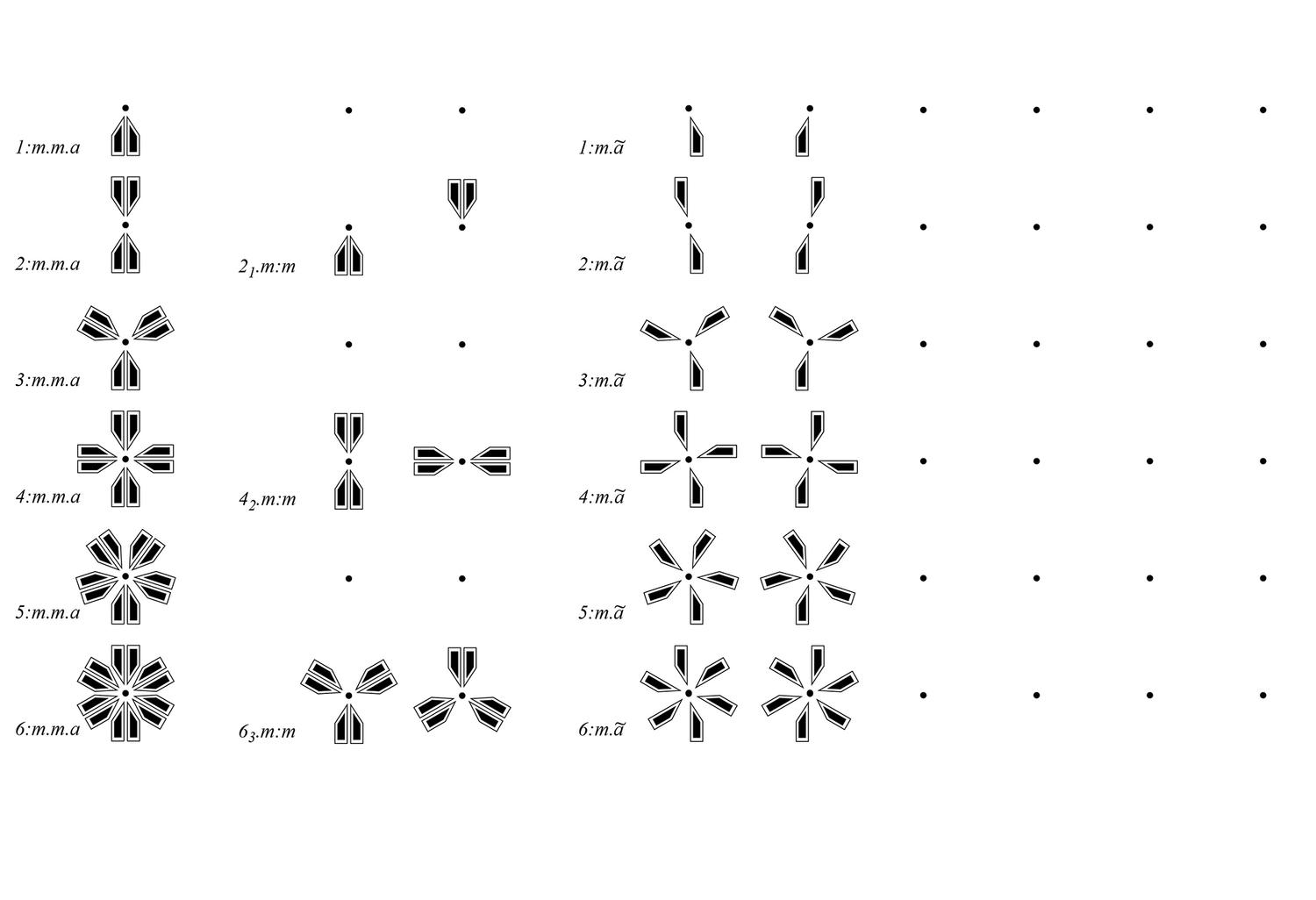
“[The] charm of impossibilities… at once voluptuous and contemplative, resides particularly in certain mathematical impossibilities of the modal and rhythmic domains. Modes which cannot be transposed beyond a certain number of transpositions, because one falls again into the same notes; rhythms which cannot be used in retrograde, because in such a case one finds the same order of values again” (Messiaen, The Technique of My Musical language, 1956). The symmetry properties of the equal temperament scale are computed here using Polya’s theorem of enumeration of non-equivalent configurations with respect to the permutation group of the vertices of the dodecagon. All scales are diagrammatically represented as colored polygons within the regular dodecagon and accompanied by their respective representation in typical western notation in their first transposition. The color in the first set of diagrams classifies the scales in terms of their number of notes and in the second set of diagrams in terms of their symmetry properties.
Acknowledgments. The illustration and sonification of the patterns has been done by Haldoun Kececigil and Heath Washburn.
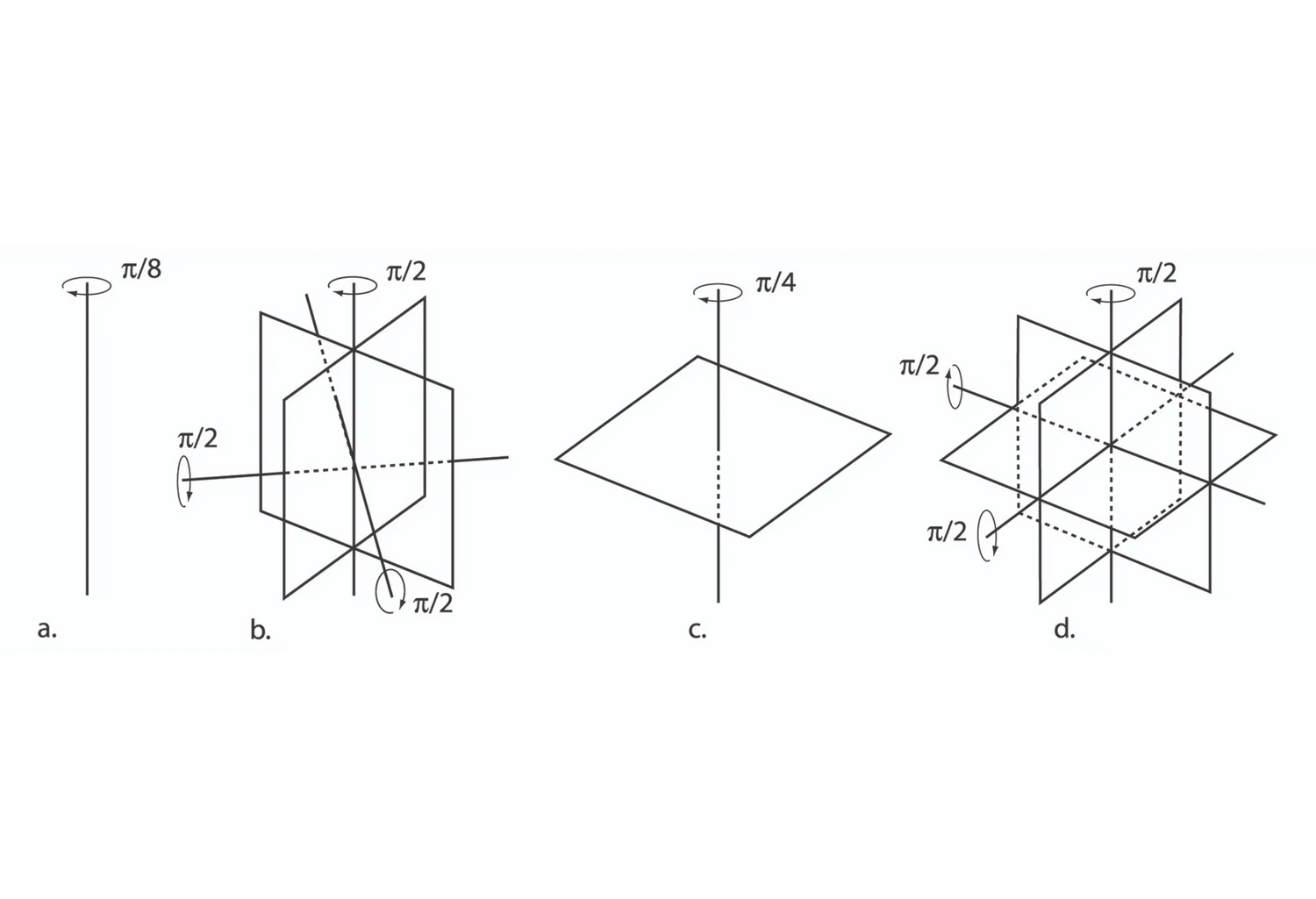
Rod Symmetry
Athanassios Economou
2006
Keywords: Shape studies; Symmetry; Linear Growth; Symmorphic groups
The project looks closely at a specific class of three-dimensional designs that have one axis of growth and presents all possible algebraic structures that capture the symmetries of these designs. A specific set of seven types of designs is discussed, the symmorphic designs, and is used as a framework to derive the non-symmorphic designs and to complete all three-dimensional linear structures. The complete catalogue of all nineteen space structures that may be generated in this manner is presented for n-fold screw rotations, n <=6.
Frit: An Enumeration of n^2-Cell Structures, for n<=4
Athanassios Economou and Thomas Grasl
2006
Keywords: Enumeration; Symmetry; Configuration; Polya’s Theorem of Counting; Recursion
A class of recursive patterns that satisfy given area coverage constraints and given patterns of distribution is specified here. The elementary models of these patterns involve four properties: a) topology, b) area, c) scale, and d) configuration. A pattern may appear to be nuclear or linear with respect to the basic topology of the repeated element in the configuration. Similarly, these same patterns may be given in the complimentary form where the figure-ground relationship between shape and background is reversed. The same topological patterns may be used for different amounts of coverages. Similarly, the same medium-dispersed nuclear patterns may be used in their corresponding linear form for different area coverages. A pattern may appear to be concentrated or dispersed with respect to the number of parts that are taken to constitute the pattern. The patterns are assumed to be continuous and isotropic and there are three geometric arrangements—triangular, rectangular, or rhombic, and hexagonal that can satisfy these constraints.
Isovox
Athanassios Economou and Matthew Swarts
2006
Keywords: Mappings; Partitions; Architecture and Music; Proportion; Isovist; Isovox; Andrea Palladio; Villa Capra
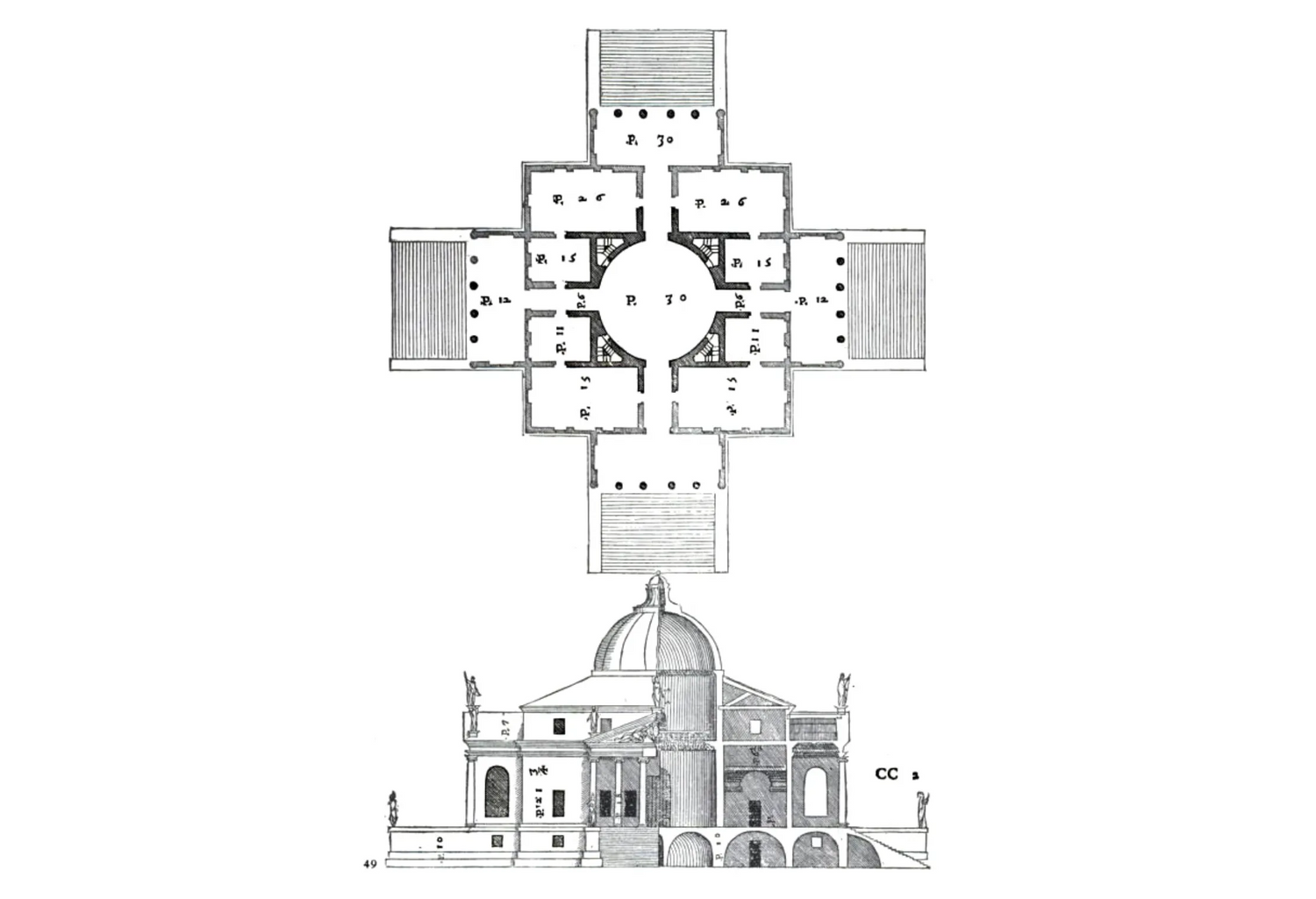
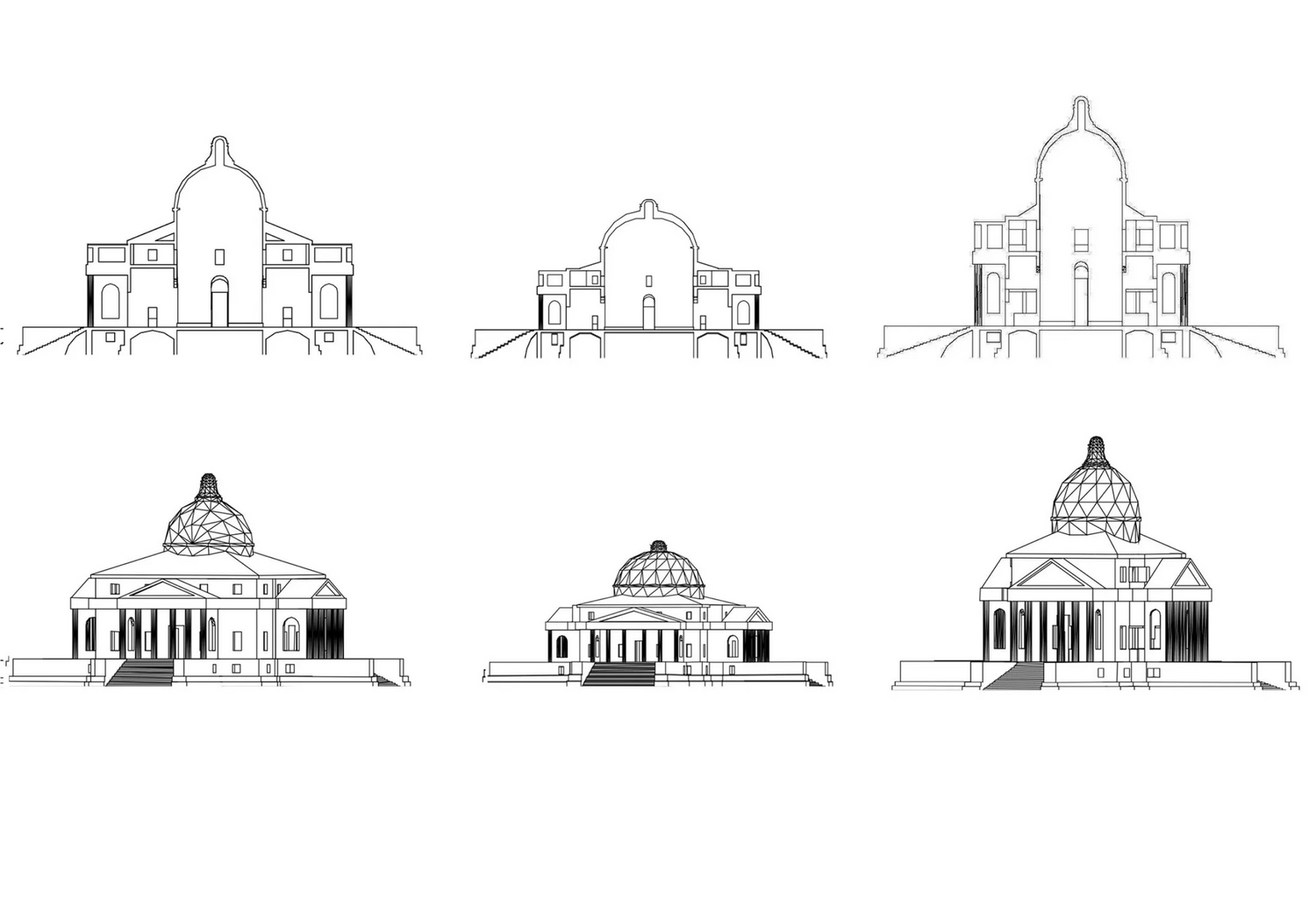
The relevance of music theory as an interpretive framework for the understanding of Palladio's work has been one of the most debated subjects in the realm of architectural theory and criticism. Typically the debate is quite abstract and it focuses on possible mappings between the ratios found in Palladio’s plans and corresponding ratios used in contemporary musical temperaments. The project here rather focuses on the actual performance of the ratios found in Palladio's work and the implications of this performance, melodic and harmonic, for the perception of the space for a situated observer/performer. To that extent the study suggests a model of mapping between space, sound and color and correlates that with polygon partition theory to simulate movement within a space. All examples to test these ideas are based on Palladio’s Villa Capra.
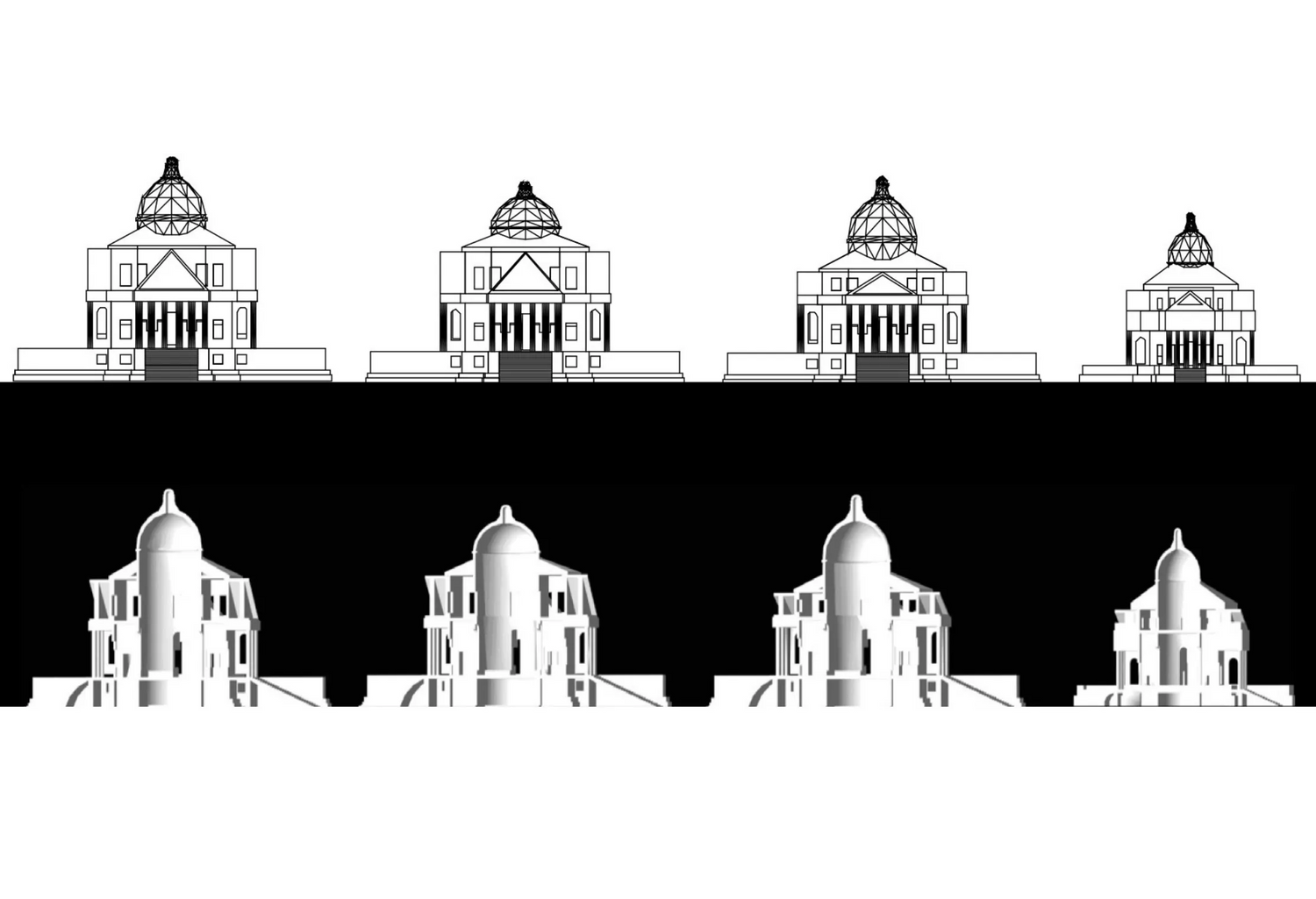
Hermes: Computing with the Eleven Proportionalities in Design
Hyoung-June Park, Panos Papalambros and Athanassios Economou
2005
Keywords: Proportion; Eleven means; Design automation; Palladio; Villa Rotunda
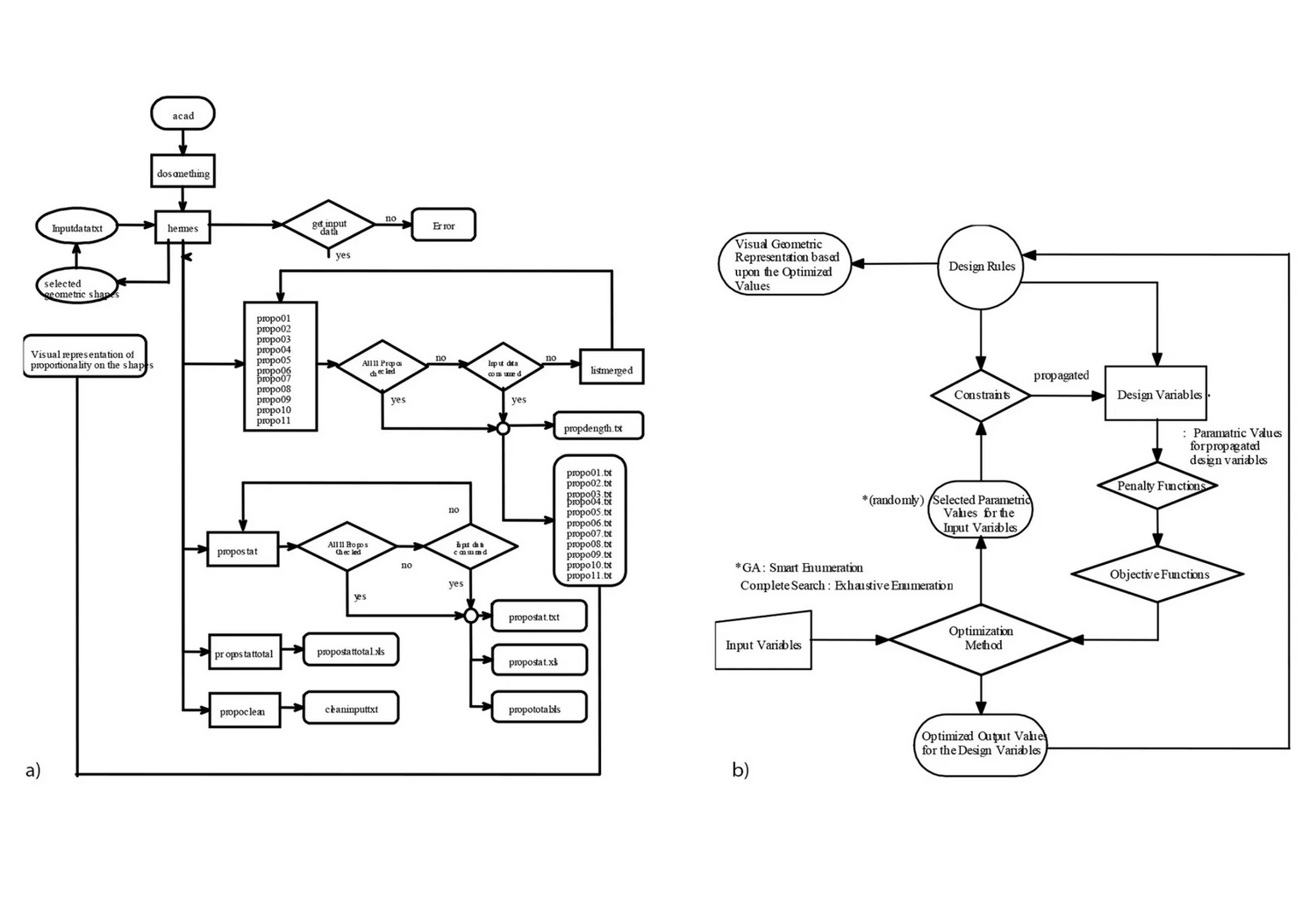
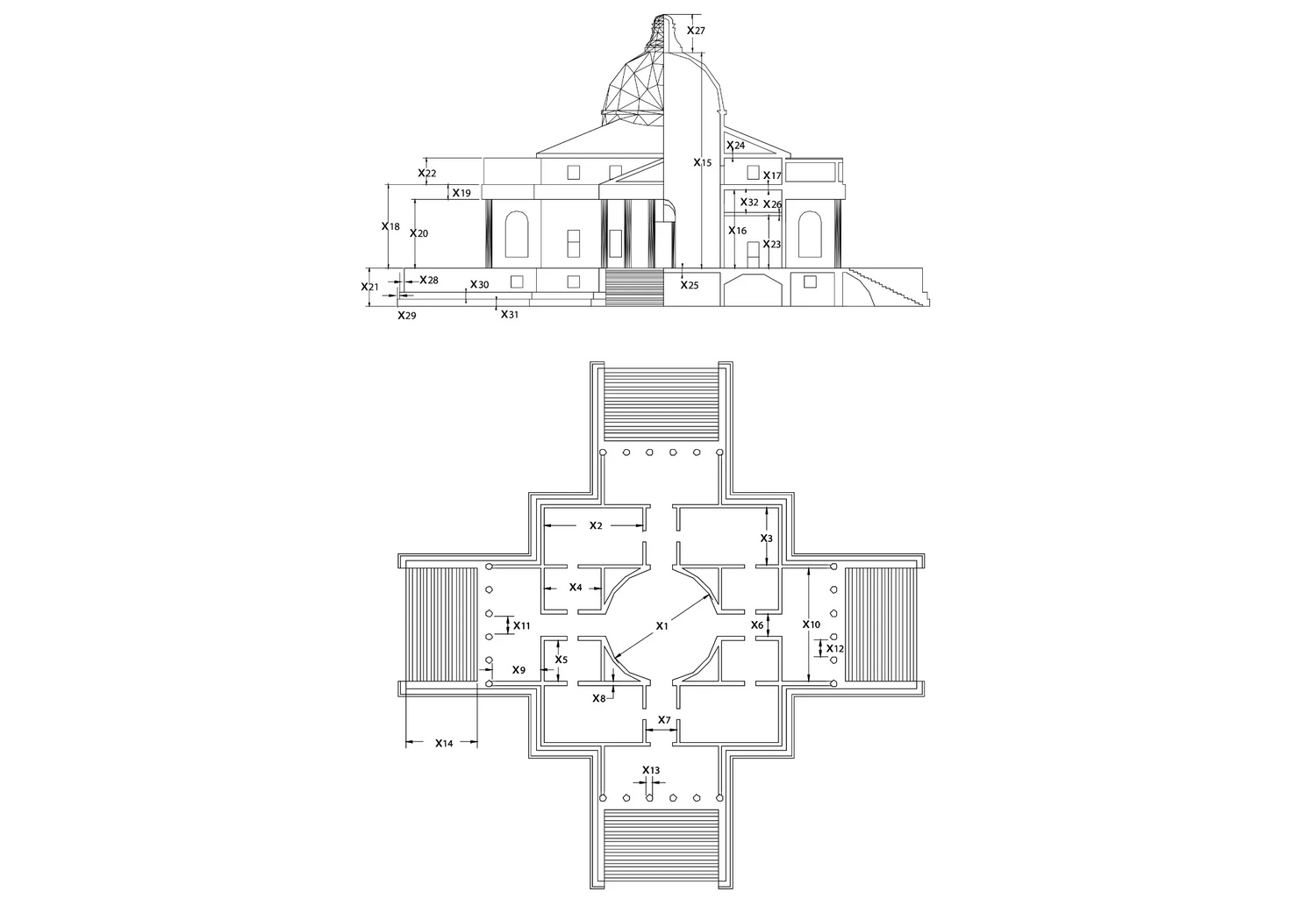
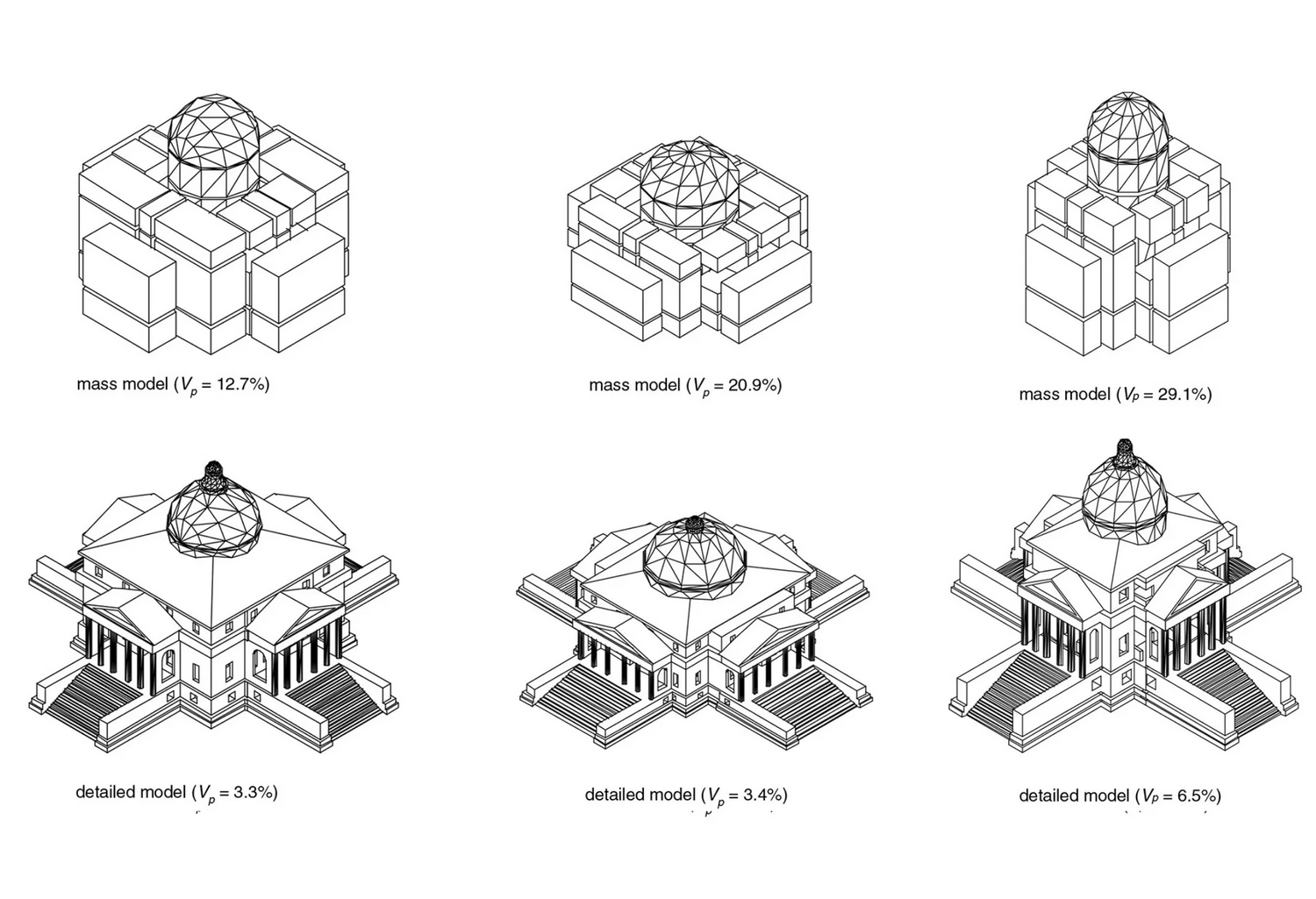
The absence of computational tools for the application of proportional theory in analysis and synthesis in design has been a persistent problem in the field of formal composition in architectural design. A computational tool, code-named here Hermes, is introduced as a tool for proportional studies based on the theory of the eleven proportional means. The analysis component of the application evaluates existing designs and provides statistical measures about the proportional structure of the design. The synthesis component of the application generates new designs from known ones with additional prescribed proportional properties. The analysis component is written in Autolisp and runs within AutoCAD. The synthesis component is written using the Genetic Algorithm Toolbox of Matlab and an AutoLisp application within AutoCAD. Both cases are built using extensively design optimization methodologies. The corpus of the designs for both analysis and synthesis has been selected from Palladio’s buildings to link this project to the long list of research projects that have tackled proportion using Palladio’s work as an exemplary body of work.
Innercube
Athanassios Economou
2006
Keywords: Symmetry; Point groups; Kindergarten method
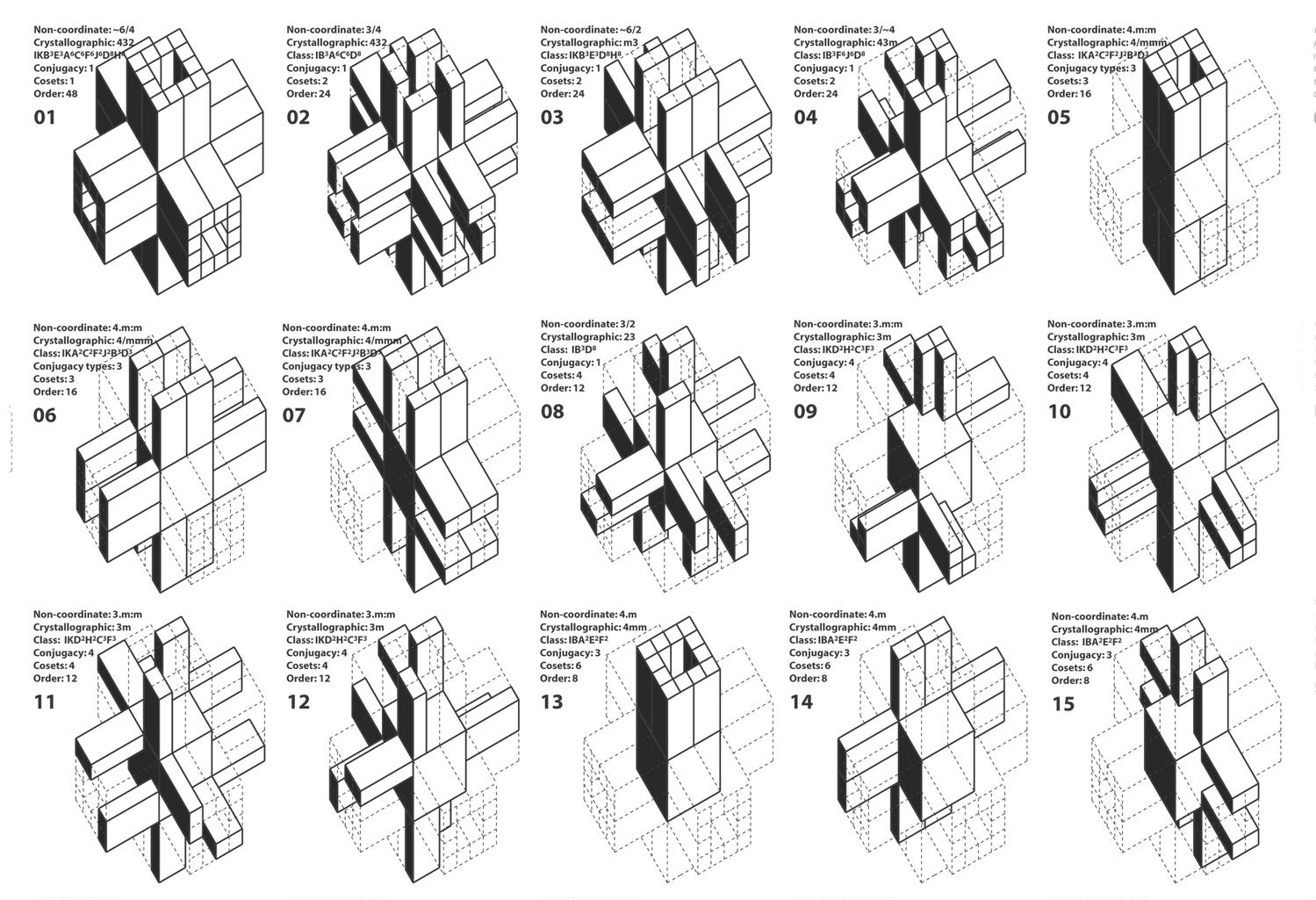
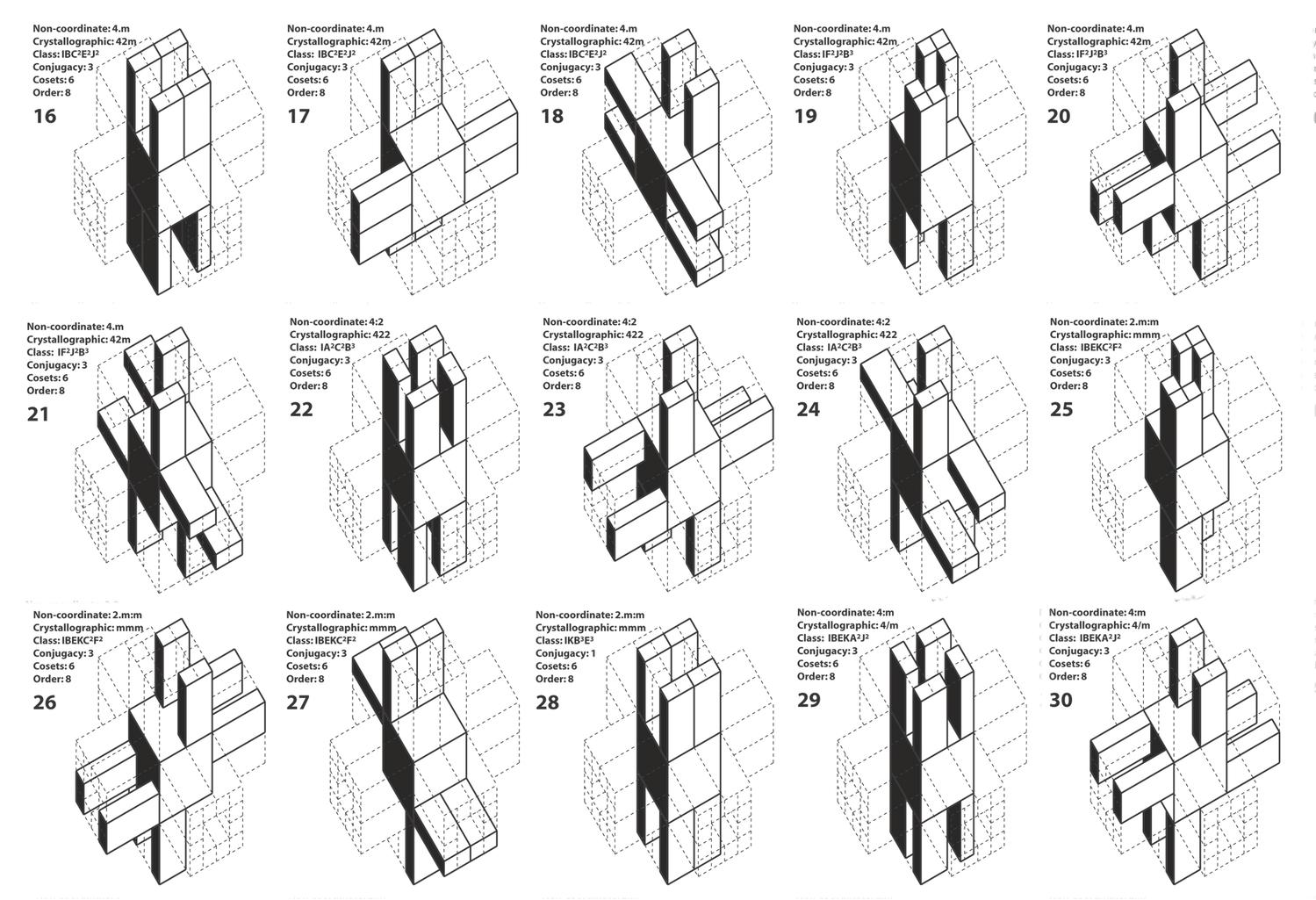
The structure of the Froebel gifts can be explored in terms of the isometries that leave them invariant. This classification is similar to the classifications employed for the partition , say, of the Euclidean group, E, consisting of all isometries, to the ten groups Eij, or the partition of the three dimensional point group , E03, consisting of all rotations, reflections and rotor reflections about a point 0, in the seven polyhedral groups and the seven infinite sets of point symmetry ; the difference is that while those classifications are built upon classes of equivalent isometries in the Euclidean space, i.e. all reflections or all n-fold rotations are of the same type respectively, this classification distinguishes between these symmetries, so far considered typologically the same, in respects to the effect that they impose on each individual spatial structure . In these corresponding spaces, neither all reflections are the same, nor all two-fold rotations are of the same type. In the cube, for example, a reflection in a face plane interchanges all three pairs of faces while a reflection in an edge plane interchanges two faces and leaves two faces still. Both isometries permute the faces in a different way and thus they are classified as different. Informally, two isometries are equivalent or conjugate when they impose the same kind of rearrangement in the structure. Formally, given elements x, y of a group G, xis conjugate toy if gxg-1 = y for some g E G. The set of all conjugates of x, {gxg-1 19 E G} is called the conjugacy class of x in G and all the elements in the same class have the same order.
Within this context the forty-eight elements of the symmetry group of the cube naturally split in ten conjugacy classes (Yale, 1988). The conjugacy classes of the symmetries of the other three Froebel blocks are subsets of these ten classes. The sixteen elements of the pillar are partitioned in eight classes, the eight elements of the oblong in four classes and the four elements of the half-cube in three classes. The explicit descript ions of these types of symmetries and their order for the four Froebel blocks are given in Table 3. These conjugate classes of symmetries combine to create conjugate groups within the symmetry groups of each individual solid. The conjugate subgroups show essentially the different types of symmetries within each block . There are thirty-three conjugate classes in the octahedral group and it can easily deduce that the symmetry groups of the pillar, the oblong and the half-cube can be further partitioned in twenty-three , eight and four conjugate classes respectively. The symmetry groups can be even further scrutinized in terms of all the distinct subgroups that are formed out of all possible combinations of the elements of the group.
The structure of the cube, the octahedral group, has ninety-eight subgroups which all together form the thirty-three conjugacy classes of the cube. All the subgroups of the other Froebel gifts are contained within these ninety-eight groups. It can be easily checked that the symmetry group of the pillar contains thirty-five subgroups, the symmetry group of the oblong contains sixteen subgroups , and the symmetry group of the half-cube contains four subgroups . The complete number of all conjugate subgroups for the cube is given here for a spatial relations between a cube and an oblong.
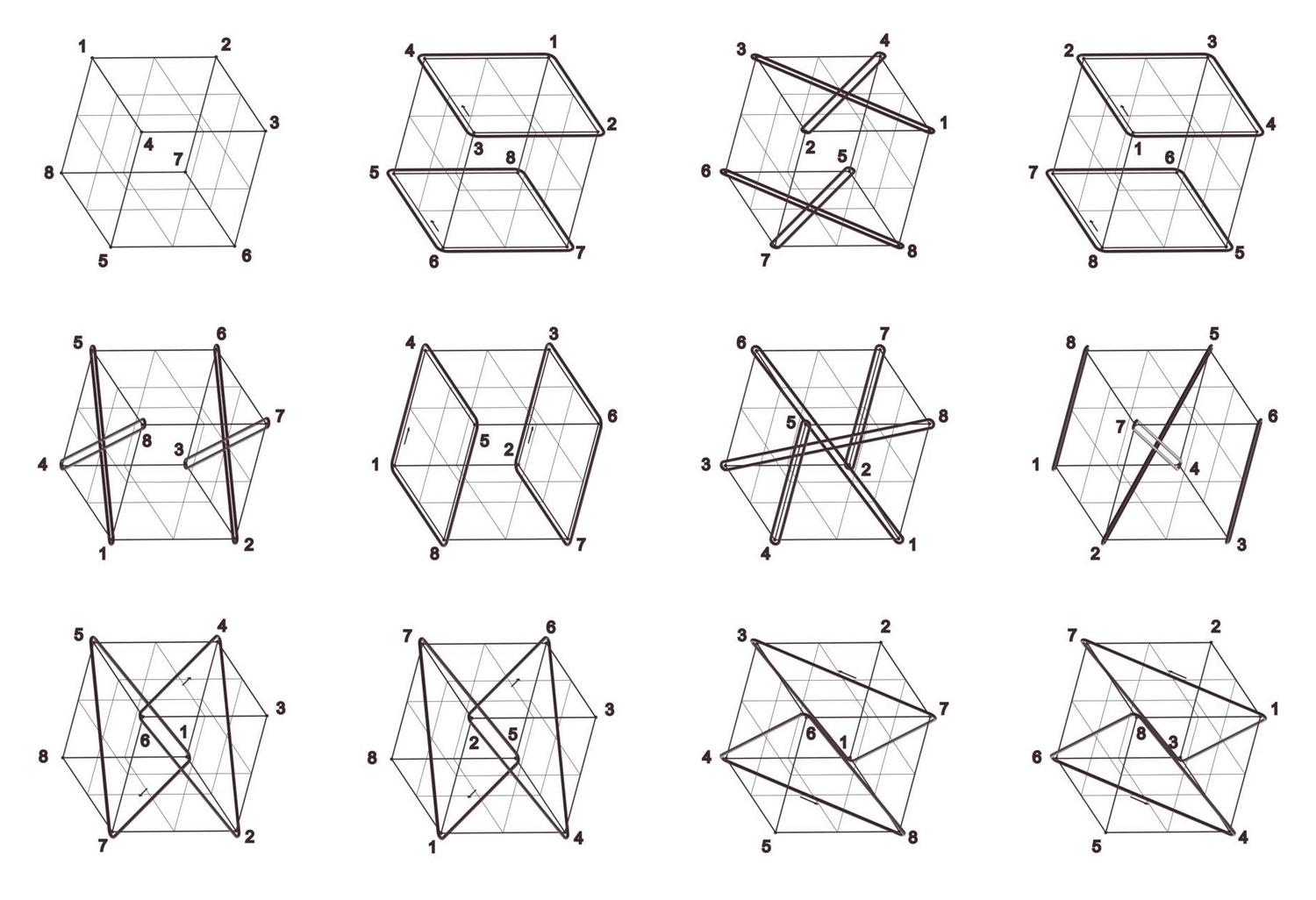
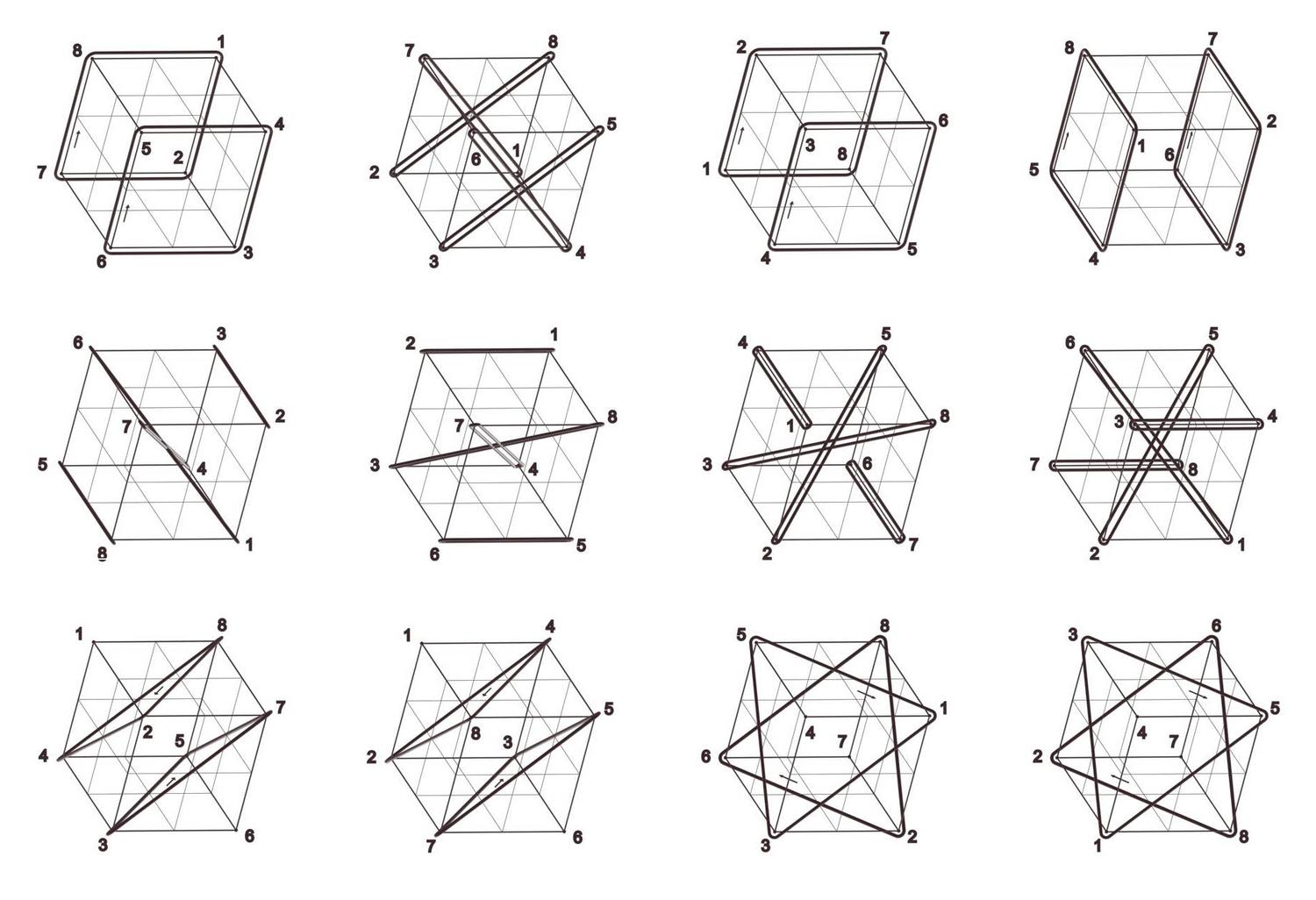
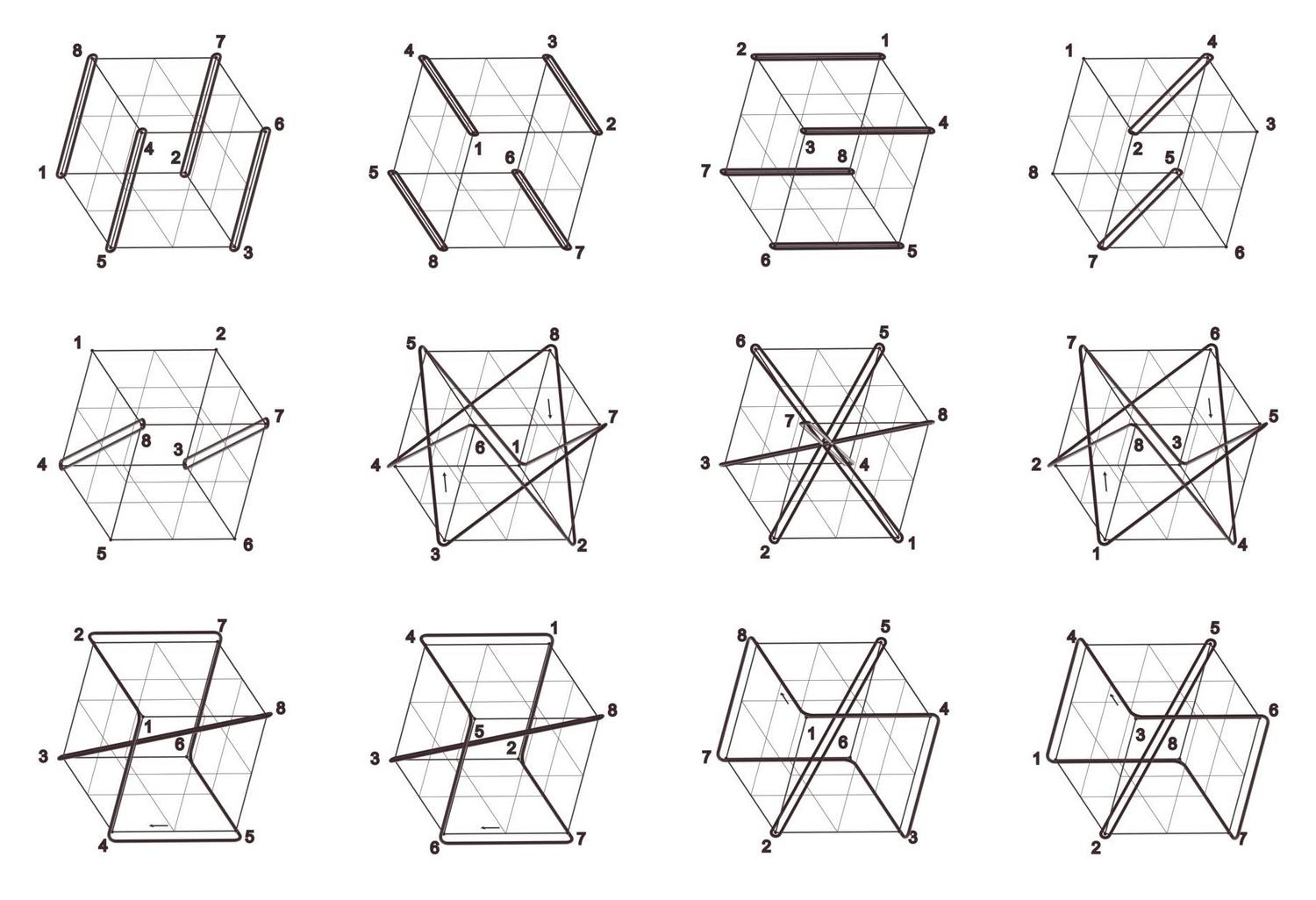
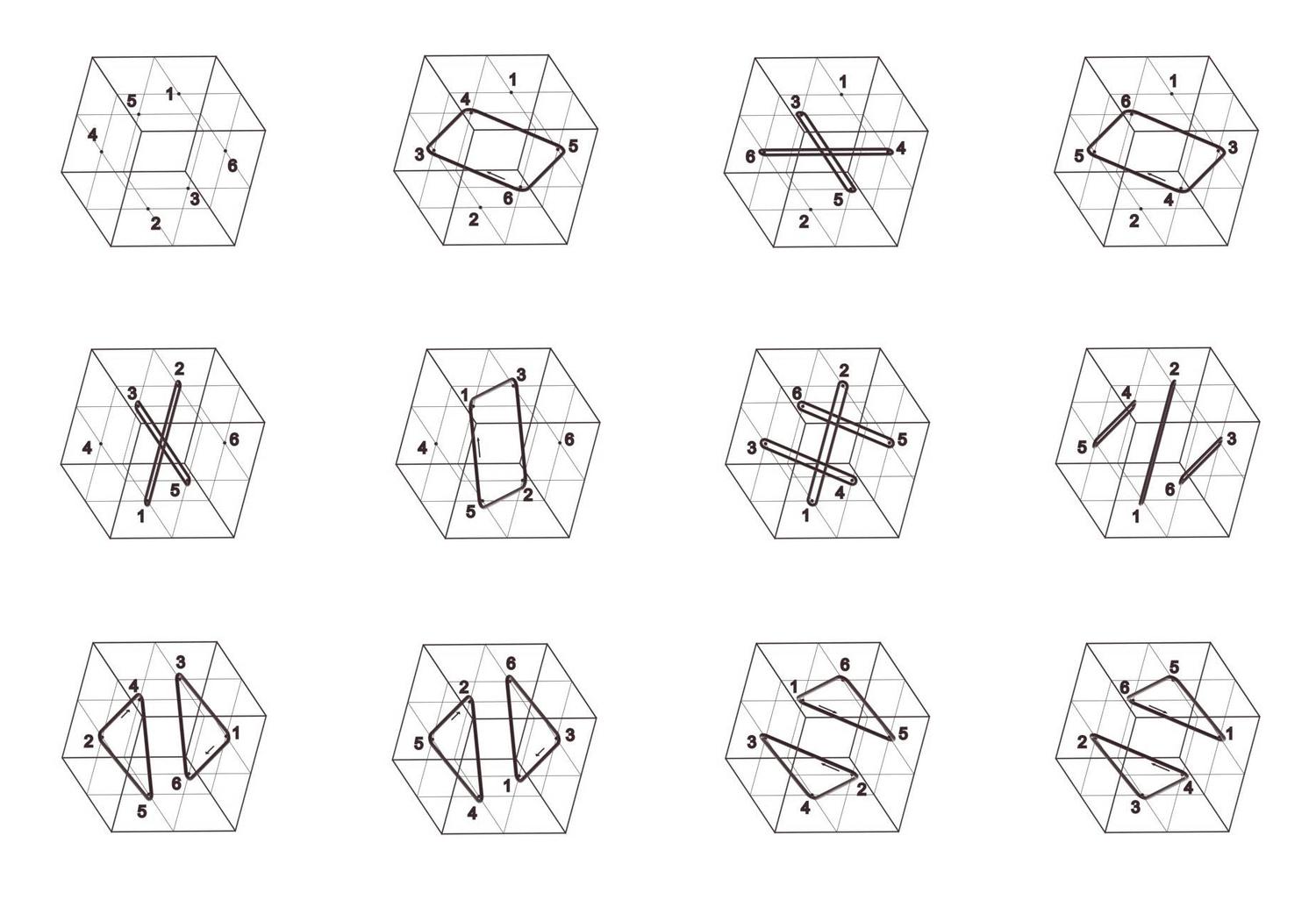
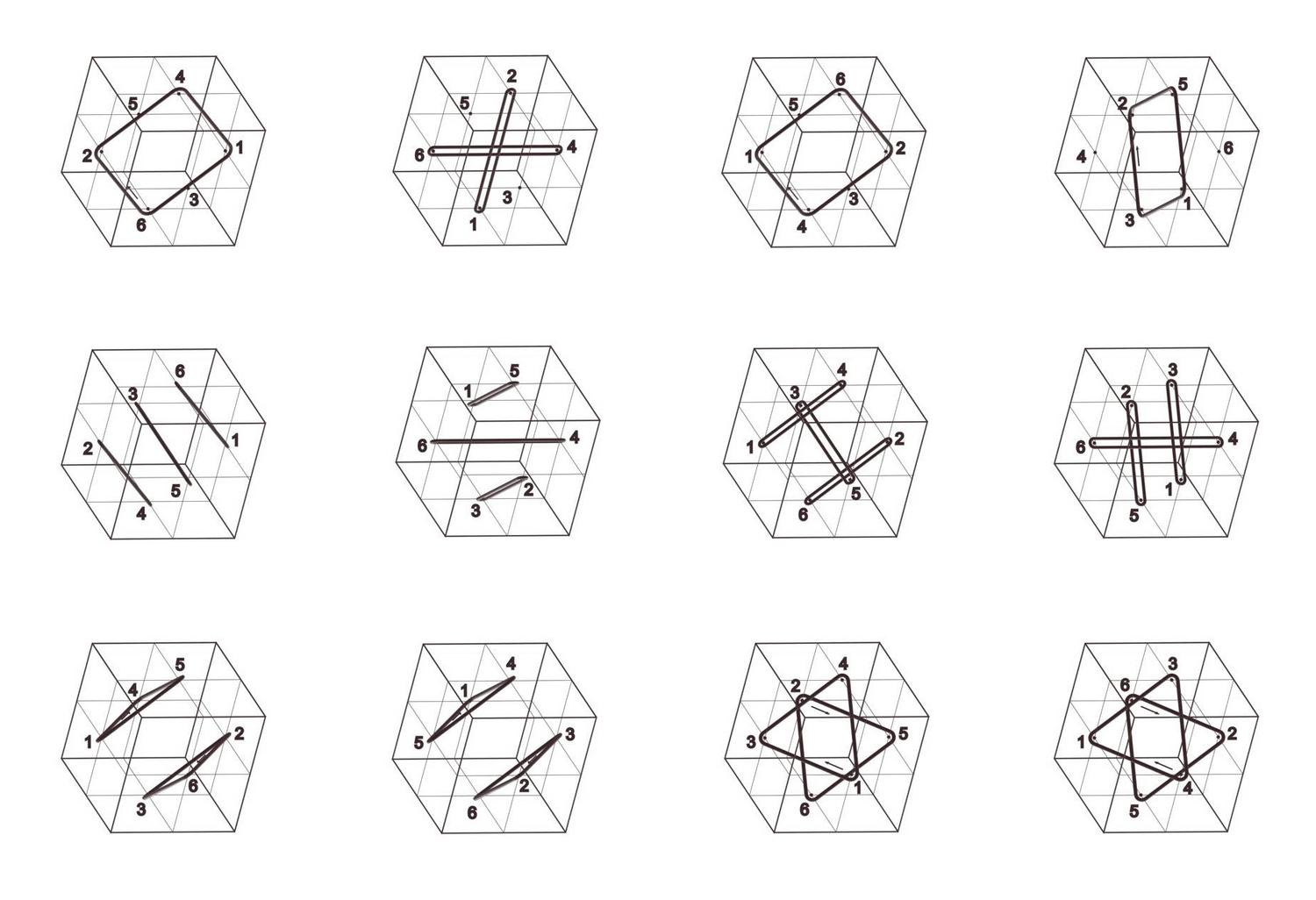
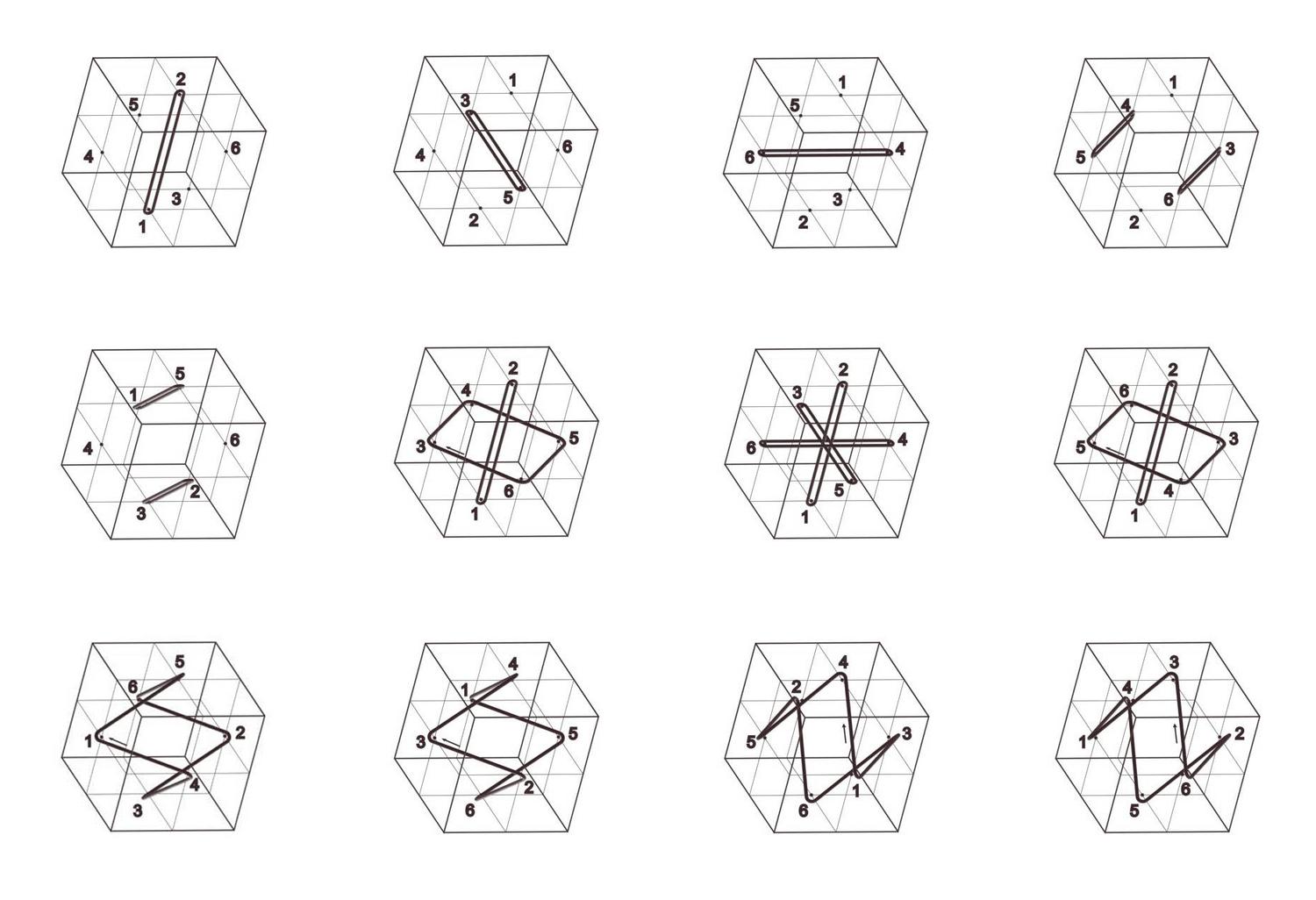
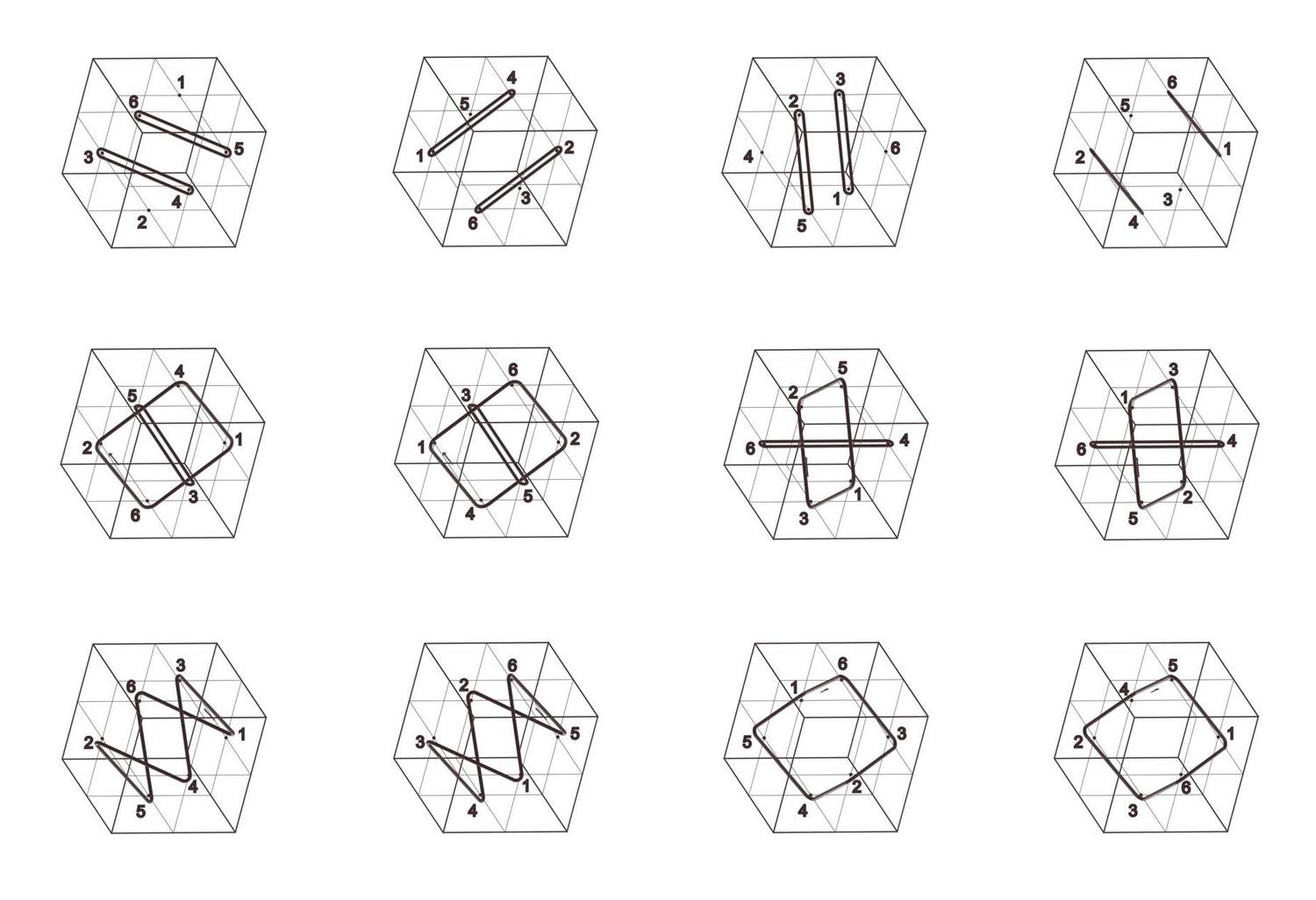
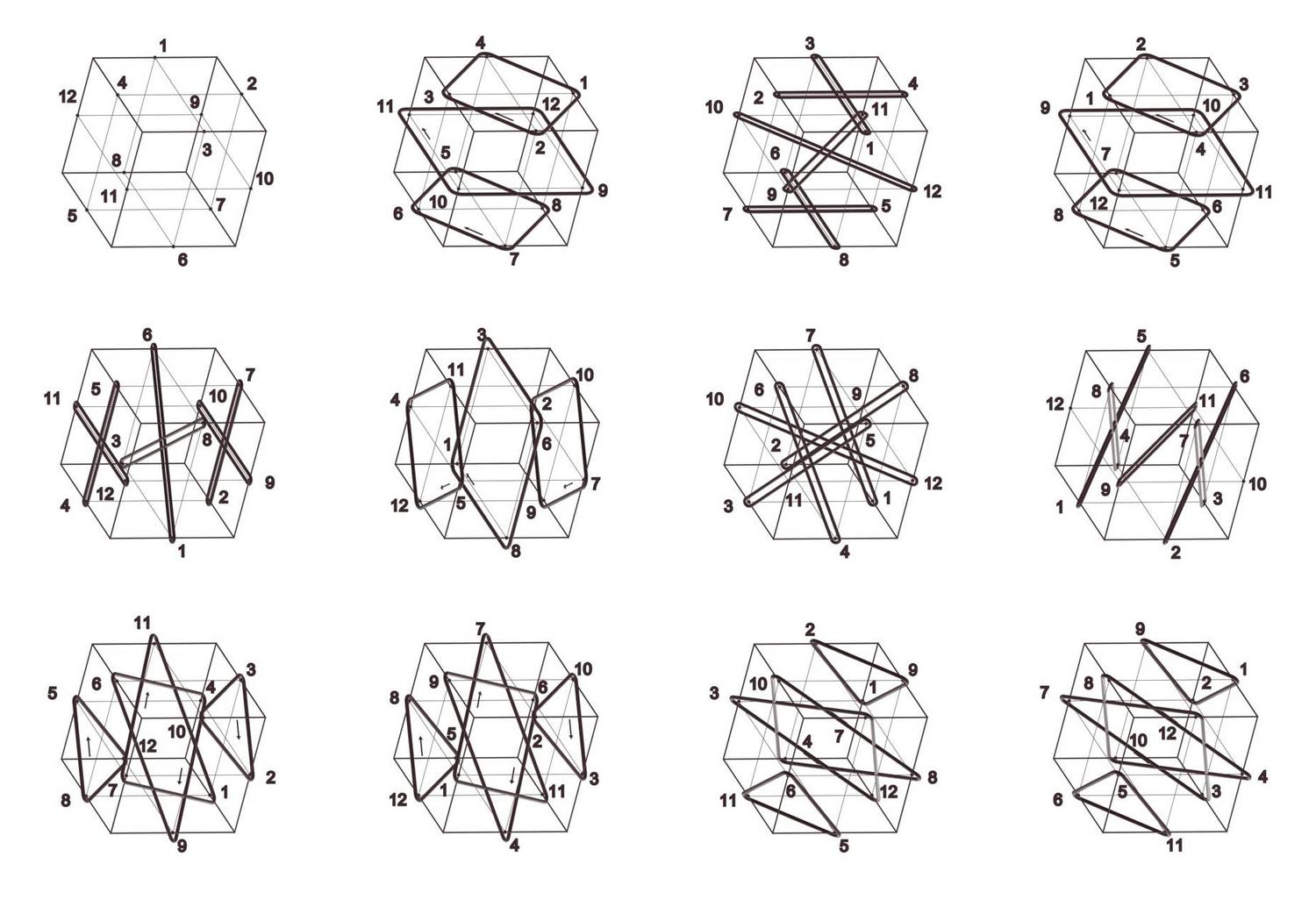
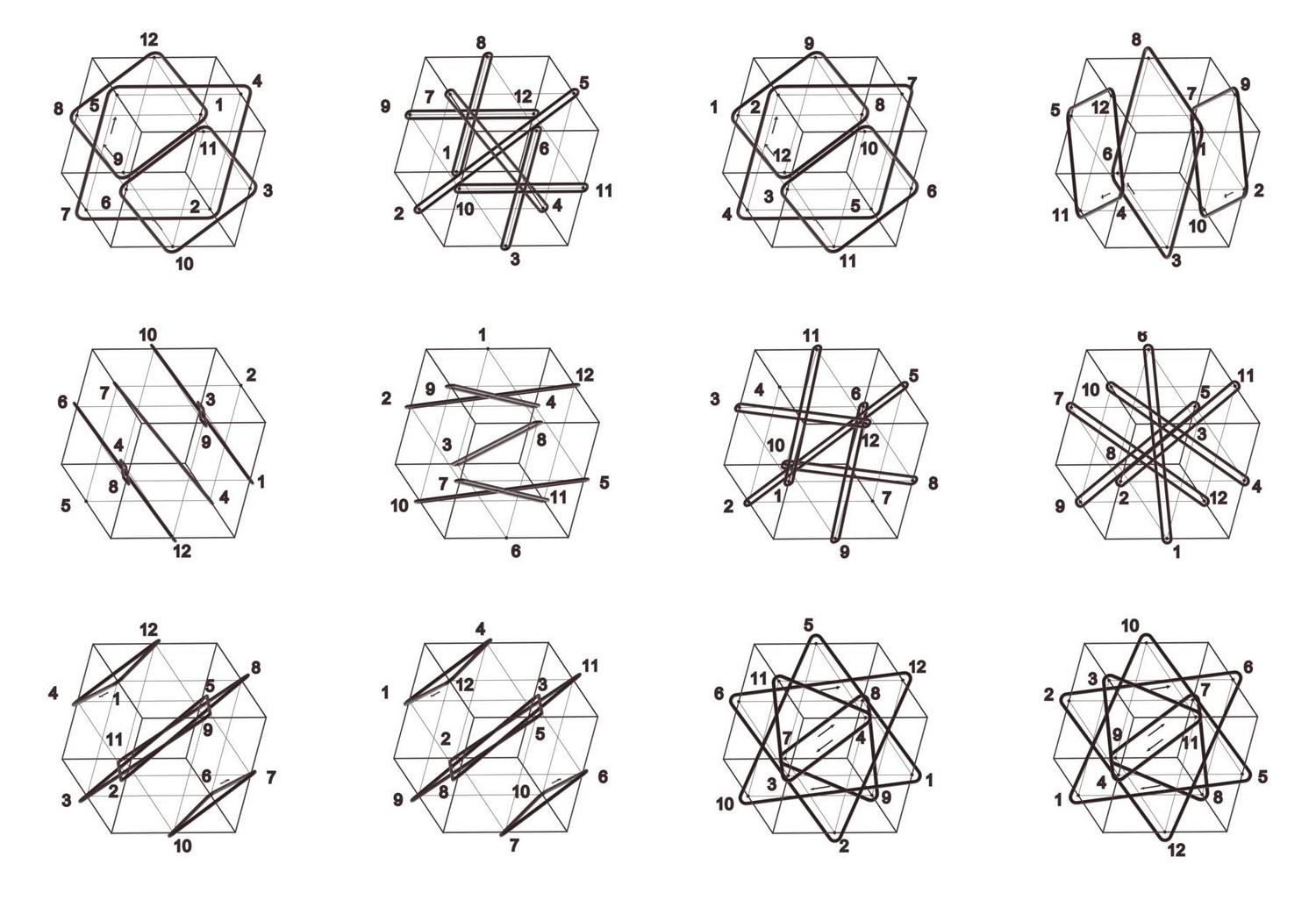
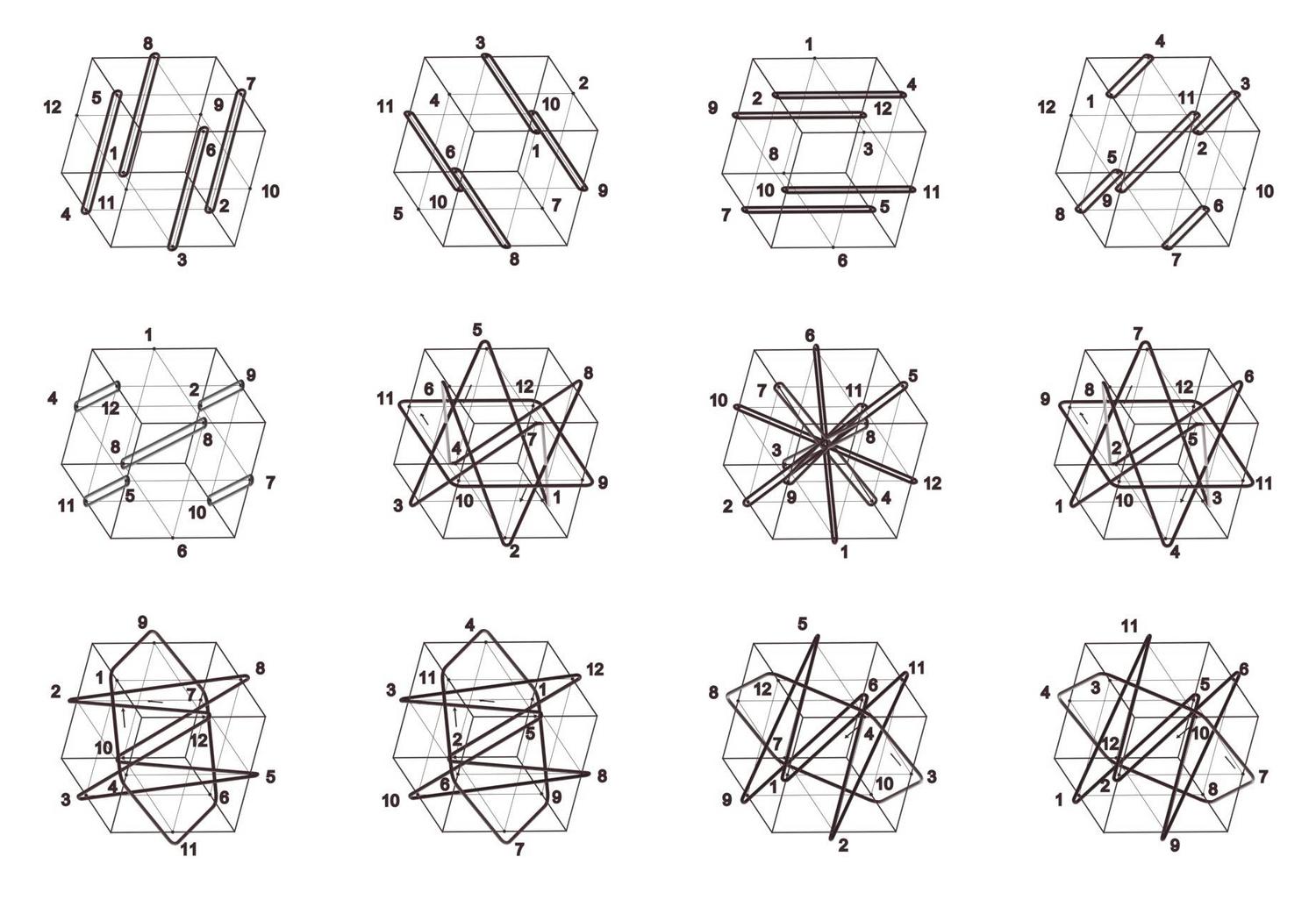
Cube Orbits
Jerry Hsu and Athanassios Economou
2005
President’s Undergraduate Research Award (PURA) Award, Georgia Tech
Keywords: Cube; Hexahedral group; Permutation groups; Cycle index; Symmetry; Configuration;
The cube has always been one of the most ubiquitous shapes in three-dimensional spatial design. Aspects of the mathematical structure of the cube have been explored with different tools drawn from Euclidean geometry, descriptive geometry, group theory, permutations and combinatorics. Here one of the most interesting visual representations of the structure of the cube is given in terms of the cycle index of the permutation groups of the vertices, edges and faces of the shape under the symmetry group of the cube. All permutations are given in a consistent projection depicting the symmetry transformation that induces them as the geometrical loci of points that remain invariant under the transformation (typically axes of rotation and rotor reflection, and planes of reflections) and the cycles of permutations of the vertices, edges and faces as closed rings circumscribing them.
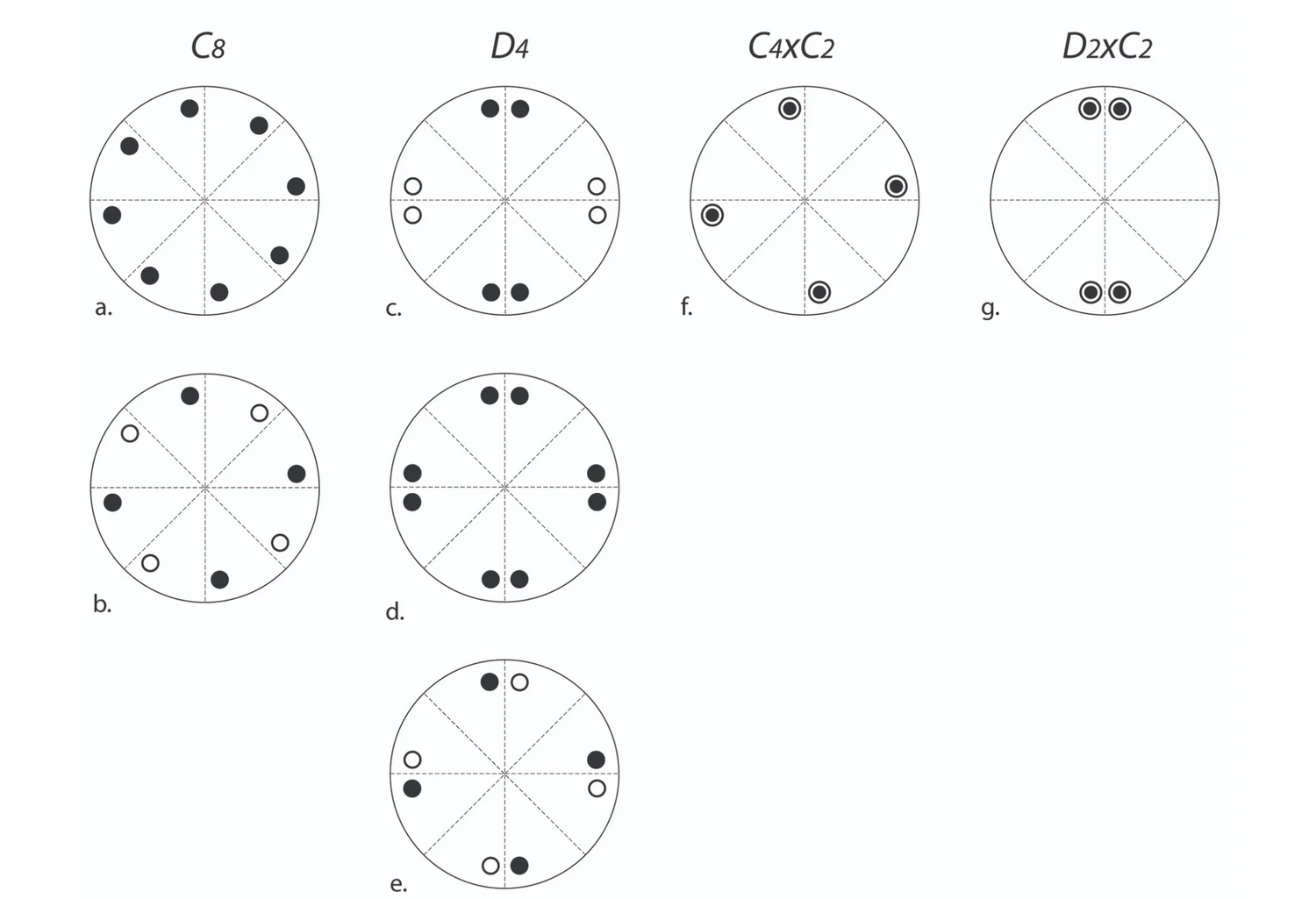
Four Eights
Athanassios Economou
2002
Keywords: Symmetry; Prismatic groups; Configurations; Shape grammars
A constructive program for the generation of three-dimensional languages of designs based on nested group structures is outlined using the four possible algebraic infinite symmetry structures of 3-dimensional space, that is, the cyclic and dihedral groups and their direct product groups, and their corresponding seven prismatic groups in Euclidean space. The pedagogical material and the studies themselves focus on a specific order, here the order 8, to showcase the expressiveness of these structures in design.